A somewhat frequent concern I see when people discuss the possibility of a
planet with multiple moons is that the combined influence of the moons could
impose harsh or chaotic tides on the planet, enough to pose a hazard to life
or societies on the surface. I figured this was an idea worth rigorously investigating,
so let's get to it.
As I've mentioned previously, average tidal height—the difference in water
level between lowest and highest points of the tidal cycle, more typically called the tidal range in reference to water specifically—can be approximated like so:
h = tidal range (any unit so long as a and r use the
same)
a = distance between centers of mass of the 2 bodies
r = radius of planet
m = mass of body inducing tides (any unit so long as M uses the same)
M = mass of body receiving tides
Emphasis on approximate here; factors like the geometry of ocean basins and coastlines, differences in latitude, and formation of resonances in water motion can alter tides, both globally and locally; this method predicts an average tidal range on Earth induced by the Moon of about 36 cm, but the actual average is about 60 cm, biased upwards by certain areas where the coastlines funnel tidal motion to create local tides as great as 16 meters. For convenience's sake, I'll stick with the calculated value.
Because of the interplay of both the Moon's gravity on Earth and Earth's own motion relative to the Moon, equal tidal bulges are imposed on both the part of Earth's surface facing the moon and the part facing directly away. The tidal cycle in water level experienced on the surface is mostly due to Earth's rotation moving points on the surface through these bulges, but the bulges also slowly move to follow the orbital motion of the moon. This pans out to a tidal period of a bit over half a day, or more generally:
Ttide = Tidal period (any unit so long as Tday and Tmonth use the same)
Tday = Day length (sidereal or synodic, so long as Tmonth is the same)
Tmonth = Month length
Note that days and months here can be either sidereal (measured in terms of absolute motion of bodies relative to the static background of stars) or synodic (measured relative to the apparent position of the sun), so long as the same standard is used for both. When calculating lunar orbit periods by Kepler's laws, they'll typically be sidereal, but the conversion to synodic is fairly easy. Retrograde rotation or orbital motion can also be accommodated if it is entered as a negative value.
Given tidal range and tidal period, the overall tidal cycle can be approximated as a sine wave with an amplitude of half the tidal range and a period equal to the tidal period:
L(t) = Water level relative to average (same unit as h)
t = Time after initial high tide (same unit as Ttide)
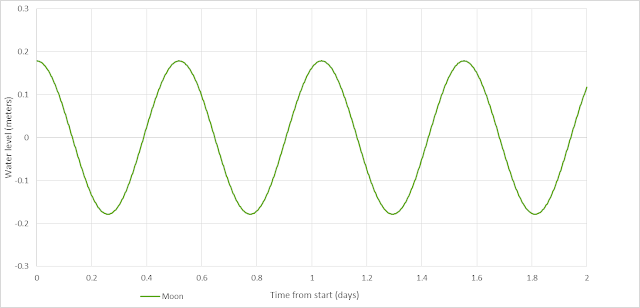
For Earth and the Moon, with a calculated tide height of 35.7 cm and a tidal period of 12.4 hours, that looks like so:
Again, complications in ocean geometry and resonances may create more complex patterns in any one area (and throughout this post I'll be ignoring the influence of orbital eccentricity, inclination, or precession for any of the bodies involved), but this'll do as a general approximation.
Now, the sun also induces tides on Earth, with a tidal range of 16 cm and a period of exactly half a day.
The water level at any one time should be simply the sum of these tidal influences.
Because of the slight mismatch in lunar and solar tidal periods, the relative timing of their respective high and low points shifts in and out of alignment, giving us our pattern of spring tides—when the cycles align to reinforce each other and give us our largest tides—and neap tides—when the cycles are exactly out of phase, partially dampening each other. This second-order cycle itself has a period of about half a synodic month. This is also accompanied by a slight shift in the timing of high and low tides, such that some tidal cycles are a bit longer than others, but it's a very subtle difference.
This already pretty well demonstrates the point that multiple overlapping tidal cycles need not lead to chaos: the lunar tides absolutely dominate over the half-as-high solar tides on a day-to-day basis, and the solar tides become evident only in longer-term patterns, though that effect is still fairly substantial. But let's see how multiple moons influence matters—though for simplicity's sake, I'll be neglecting the solar tides from here on out (in general it adds a bit of noise to these cycles but doesn't substantially alter their overall shape).
Say Earth had a second moon, equal in mass to our existing Moon and in a 1:2 orbital resonance with it; one moon orbits with twice the period of the other. First, let's place this new moon outside the orbit of our own, at 159% the distance, for an orbital period of 54.6 days (but a synodic month of 64.3 days). The greater distance pans out to a tidal range of a mere 9 cm and period of 12.2 hours. This is just a minor modification on our existing tides, and really probably would be hard to notice against the effect of solar tides.
Now let's place the new moon within the orbit of the existing one, at 63% the distance for a period of 13.7 days (a synodic month of 14.2 days). This gives a rather more impressive tidal range of 142 cm, which then dominates over our existing tidal cycle.
This seems to be the typical pattern: because tidal range depends so strongly on each moon's orbital distance, the innermost large moon usually dominates over all the others, with other moons just modifying the amplitude of that cycle.
But there are some specific cases that place moons on more equal ground. For one, a pair of moons could share an orbit as mutual trojans spaced 1/6 of an orbit apart, thus exerting relative tidal influences in proportion to their relative masses, but as it turns out for equal-mass moons this balances out to yield a single tidal cycle effectively equal to what you would from a single moon with about 86% of their combined mass, with high tide when the two moons are at about equal height in the sky.
More complex tadpole or horseshoe orbits may involve more complex patterns of moons shifting in and out of phase, but generally work out to something like our lunar+solar tidal cycle of periodically stronger and weaker tides rather than anything more complicated.
Returning to separate orbits, if we can take the inner moon from our latter 1:2 resonance case above and reduce its mass to 1/4 that of our Moon (a bit less massive than Triton), that neatly balances out to give it the same induced tidal range as the outer moon. Tidal amplitude then varies pretty significantly over a cycle lasting about as long as the orbital period of the inner moon, bouncing between a double-strength tide with a range of over 70 cm and then a brief period with essentially no tides.
What about a third moon? Let's pull the same trick as above again and place a moon 1/16 the mass of our original one (a tad larger than Haumea) in a ~7 day orbit, such that the whole trio follows a 1:2:4 Laplace resonance like the 3 innermost Galilean moons. There are a couple different possible configurations—the Galilean moons are offset so that no more than 2 moons are in conjunction (in the same direction from the planet) at any time, but the planets of Gliese 876 have a Laplace resonance that does allow for triple conjunctions—but ultimately these work out to the same tidal cycle, a funky 3-part tidal cycle with occasional peaks in tidal range of up to a meter when all 3 moons align in either conjunction or opposition (on opposite sides of the planet), but a more typical average of around 40 cm, with highs and lows not following the motion of any one moon in particular and a period between high tides ranging from about 13.4 to 16.4 hours.
This does depend on a neat coincidence of masses, though; if the new moons are respectively 1/2 and 1/4 the mass of the original rather than 1/4 and 1/8, there's still a notable variation in amplitude and occasional oddball cycles weaker or stronger than the rest, but the overall cycle hews rather closer to the orbit of the innermost moon.
In all these cases so far, the general shape and period of any one tidal cycle varies little, just its amplitude. That's largely because Earth's rotation is so fast compared to the orbits of these moons that it controls the tidal cycle, and all 3 moons have similar tidal periods with just slight offsets.
Let's say we shifted our trio of moons down to half the orbital distances, adjusting masses as necessary to keep all the same tidal ranges (making the outermost moon smaller than Pluto and the innermost smaller than Tethys). The outermost moon (with a ~10-day month) still has a fairly short tidal period of 13.3 hours, but the innermost has a tidal period of 20.3 hours (lengthening Earth's day would have a similar effect but this way helps keep all the timescales fairly short). The resulting tidal cycle is rather more eclectic, with a couple oddly long cycles (over 21 hours between high tides) and rapid jumps in tidal range, such that one cycle can be as much as 3 times greater in amplitude than the next.
Shift the moons to 1/4 their original distance and the tidal period of the innermost is now over 3 days (because its close to geostationary orbit and its orbital motion now just outpaces the planet's rotation); We now get a number of peculiar cases where the tides seem to briefly reverse coarse partway through a tidal cycle, or at other times we see intervals of generally low tides occasionally punctuated by leaps to extreme highs or lows.
With the moons at 1/8 their original distance—about as close as they can get before the innermost runs afoul of the Roche limit, and with masses now shifted such that even the outermost moon is smaller than the asteroid Pallas—the individual tidal periods have diverged to 5.2, 18.6, and 66 hours (and now the innermost moon has the shortest rather than longest tidal cycle, having passed well below geostationary orbit). Whether or not the oceans would actually follow the speed of the shortest cycle is up for debate, but presuming they do, we get a rather busy result with a constant rapid shift in water level caused by the inner 2 moons superimposed over a more gradual day-to-day shift in averages set by the outermost moon.
If we feel like tweaking the masses a little again (in this case increasing the mass of the outermost moon and reducing the innermost), we can also get similar cycles that are less hectic but still exhibit a jerky motion that might appear a bit odd to the unfamiliar beachgoer.
Imposing though this may appear, ultimately I don't think it's especially hostile. Given how well we handle contrasts between spring and neap tides--to the point that most people even on coastlines probably don't usually notice the difference--and some areas weather tides an order of magnitude or more stronger than the average, I doubt these more irregular cycles would really be much more hazardous in general. Of course, I have been keeping all these tidal cycles fairly small for purposes of comparison. A large, close moon might impose much higher tides, but that's true of a single moon as much as multiple. As I've discussed before, tides are somewhat self-limiting; a moon that imposes high tides on the planet will also tend to more quickly drag the planet's rotation into alignment with its orbit until they mutually tidal-lock, at which point the ocean tides effectively stop (a tidal bulge still exists but is static relative to the planet's surface, and given time the crust will deform to fill that bulge to the same extent as the oceans, so you won't get anything like a permanent high tide). If there are multiple moons with similarly large influences (or a moon and the star), this could sort of trap the planet in a case where it can only lock to one body and will still experience ocean tides from the others, but this requires a fairly specific set of circumstances, and would also probably lead to rapid orbital migration of one of the moons, such that this situation would be unlikely to persist for billions of years.
But even if not generally hazardous to life on the planet, such tides can still have interesting consequences: before engines, ships often relied on tides to help pull them out of or into harbors where they might not be able to use their sails, and on flat coastlines tides can sometimes be locally hazardous when they move too fast to be outrun; keeping close track of the motion of the moons or just having a keen sense of the patterns of the tidal cycle could be valuable skills in such a setting, allowing someone to know when some areas might be safe to travel and when naval expeditions are best launched.
As a final note, doubles or trios of moons outside of resonant orbits can have even more complex tidal cycles, but are a bit trickier because they have to be much more widely spaced for orbital stability and so require an even more precise coincidence of relative masses to have similar-strength tidal cycles such that no one drowns all the others out. Pair our existing Moon with another at 1/5 its orbital distance (~1/11 the period) and exactly 0.8% its mass (such that they're separated by just over 8 mutual hill radii—a good rule of thumb for stability—and have equal tidal ranges) and you get this jaunty cycle:
But shift the smaller moon's mass an order of magnitude either way and the effect is largely lost as one moon dominates over the other:
Which I suppose is the main takeaway today: for most cases, you don't need to worry too much about the overlapping tidal effects of multiple moons because one will just dominate over the rest—but if you do want more unusual tides, you can get there if you tweak things just right, and I've only just explored a small range of the possibilities today.
For those interested, this spreadsheet contains all the necessary formulas to make tidal charts like you've been seeing throughout this post.
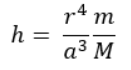

















Another excellent post. Your experiments track pretty well with my own efforts to calculate average tides for my inhabited planet, although I set mine up in Desmos instead of Excel.
ReplyDeleteGreat post, it was really helpful for me but it left me with a question: Consider a habitable moon orbiting a planet, the moon is tidally locked which would usually stop the tides but would the effects of excentricity create tides again? Since the gravitational pull would be variable across the orbit.
ReplyDeleteSignificant eccentricity could indeed create varying tides, due both to the varying distance and libration of the planet and moon
DeleteHow about tides on the moon caused by other moons? Or, in very tightly packed planetary systems, caused on a planet by other planets? Is it possible for those to be significant enough to notice?
DeletePotentially, but you'll need a more detailed model of tides to properly account for how oceans would respond to these more complex cases.
Delete@TermiteSquidSnowLeopard In systems like that, you're often going to have a relatively sharp peak in the tidal force as the planets or moons pass each other. I did some very back-of-the-envelope calculations of the energy dissipation rate of the Earth's tides a while back, and the upshot of it was that the dissipation rate was on the order of a day for the Earth. I'd figure that planet-planet or moon-moon tides couldn't really be "much" faster than this for an earthlike world regardless of the duration of the conjunction (the tidal energy would spread out and be absorbed less efficiently), but @Worldbuilding Pasta is absolutely correct that determining this quantitatively would need a more detailed model (likely including continent geometry etc.) which might be pretty hard to implement.
Delete@anonymous also it's sadly paywalled, but here's an article that discusses Titan's tides due to eccentricity in its Saturnian orbit! https://link.springer.com/article/10.1007/s10236-010-0285-3
Deletehttps://arxiv.org/pdf/physics/0701301
ReplyDeleteThanks for all of these explorations, I've had a lot of fun following along. I've left a few tide-related comments here in the past and I just thought I'd suggest ICON-O if you were interested in modelling tides in more detail? It's open-source now, and definitely modifiable if you know FORTRAN. It should be able to calculate tides ab-initio, though I haven't yet tried myself -- I'm not sure how many cpu-hours it needs for a sensible result, but here's a link to a paper. https://gmd.copernicus.org/articles/16/5179/2023/gmd-16-5179-2023.pdf
ReplyDeleteAbsolutely no pressure intended, but if it sounds interesting and not too difficult to try out I'd love to see a climate explorations using different potentials on earth's coastline!
What exactly is paywalled? The spreadsheet should be open for anyone to download
ReplyDeleteWow this is incredibly helpful! Amazing work! I'm curious, is there a mass configuration of moons that is most stable? Like, does it matter that the moon with the smallest mass or greatest mass is closer to the planet? Also, to an observer on a given planet, is it the sidereal or synotic orbit that we observe? And which is important for calculating orbital resonances?
ReplyDeleteOrbital stability is a complicated interplay of many factors, if you look at Part IVa of the main series here I've tried to lay out some of the influences but there's no easy test for any particular case or obvious difference between stable and unstable configurations. In general the tendency in the solar system is for large inner moons and smaller outer moons, but that has as much to do with how moons forms as orbital stability, and there also seems to be a population of very small moons on very close orbits.
DeleteThe synodic period is what you see on the surface in terms of the cycle of lunar phases, but the sidereal orbit is what matters in terms of the orbital physics.
What’s the largest apparent size a moon can have from the perspective of observers of the planet before tides become too strong for the planet to be habitable? Assume no mutual-tidal locking and assume the planet and moon are in the earth-like habitable zone.
ReplyDelete*observers on the surface of the planet
DeleteThis is a complicated problem in general -- the size of the tide can also strongly depend on continent positioning, day length / tide cycle length and the like. Assuming the effects of these were somehow held constant, the size scales with the cube of the apparent diameter. I'm not an authority on this but my intuition is that 100-1000 times earth's tides would limit land habitability (though ocean habitability would likely be "fine" until thermal heating was an issue). So, the moon could then be no more than 5 degrees in angular diameter (10x earth's moon) with these fuzzy numbers.
DeleteWhy isn't this spreadsheet listed with the rest of your stuff under tools and resources?
ReplyDeleteBecause I've been forgetting to update that list for like a year or two now
DeleteThis thing is view only. How do I make it work?
ReplyDeleteThere should be an option to download it.
DeleteI've been banging my head against the wall with tides for a while now, and this is exactly what I needed - thanks so much for sharing!
ReplyDelete