This will be a pretty short post, at least by the standards I’ve set so
far. I just want to make sure we’re all on the same page regarding how orbits
function and what terms we use to describe them. Probably the easiest way to
learn this is by playing a game like Kerbal Space Program, but that’s not everyone’s
preference and they never bother defining a lot of the important terms (and their patched-conics model doesn't simulate some of the more advanced concepts here). So:
Concept
The classical thought experiment to understand an orbit is Newton’s cannonball. Imagine that you
have a cannon standing in a perfectly flat plane with the barrel perfectly
parallel to the ground, and that there is no air resistance to worry about. To
start out with, imagine that we let a cannonball tip out the end of the cannon.
It has zero initial horizontal velocity and no horizontal forces acting on
it, so it doesn’t move horizontally. It also has zero initial vertical
velocity, but it has gravity acting on it to pull it down, so it gains vertical
velocity and fall downward, hitting the ground after a specific period of time determined
by its initial height and the acceleration of gravity (quick review on kinematics—the mathematics of motion—here1 if you need it).
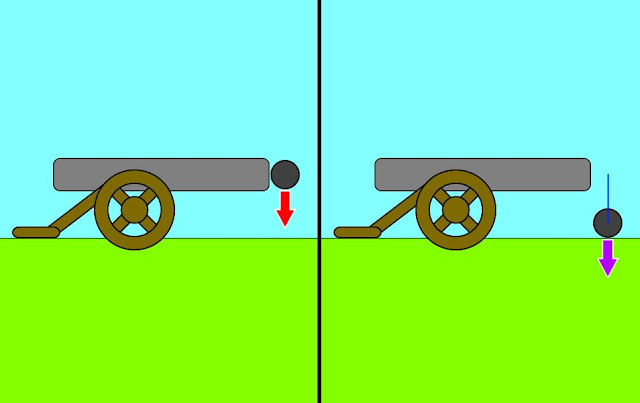 |
Cannonball at the start and end of its flight. The red arrow shows the acceleration by gravity, the purple arrow the velocity at the end of the flight (and the start in later images) and the blue line shows the path of travel. Image by me, from back when I hadn't learned not to use garish color schemes yet.
|
Now imagine that we fire the cannonball, giving it some initial
horizontal velocity but no vertical velocity. Once the cannonball leaves the
barrel, it still has no horizontal forces acting on it and only gravity acting
on it vertically, so it will take just as long to hit the ground as the first
cannonball. But it continues to move horizontally as it falls, so it hits the
ground at a different point.
Keep increasing the initial horizontal velocity, and it never increases
the time it takes to hit the ground—but it does allow the cannonball to travel
farther before it does.
Next imagine that the cannon is not on an infinite flat plane, but rather
on a perfectly spherical planet. As the cannonball travels, the ground curves
away, so in effect the cannonball has to travel a greater vertical distance to
hit the ground the farther it travels from the cannon.
But of course the direction of “down” is changing as the ground curves, so
the direction of gravitational acceleration changes as well. If we rotate our “vertical”
and “horizontal” axes to compensate, then in effect, some of the cannonball’s
horizontal velocity becomes upwards vertical velocity, and some of the
downwards vertical velocity becomes more horizontal velocity. In this rotating
reference frame, it’s as if there’s a constant upwards acceleration (centrifugal acceleration) opposing
gravity.
 |
| Path of a cannonball fired at 6 kilometers/second from a high perch on Earth. Lookang, Wikimedia You can also play with making your own paths here. |
Thus by increasing the horizontal velocity we can keep the cannonball
aloft for longer, allowing it to travel further around the planet. As we keep
increasing the initial velocity eventually we reach a point where the ground is
curving away from the cannonball as fast as it falls—in the reference frame of
the cannonball, centrifugal acceleration has matched gravitational
acceleration—and the cannonball travels all the way around the planet and
smashes into the back of the cannon (if the planet isn’t rotating). If we
diligently moved the cannon out of the way before this happened, the cannonball
would continue circling the planet forever (or as good as), losing neither
altitude nor velocity (we are of course also not accounting for air resistance, which would slow the cannonball and cause it to fall were it fired in the atmosphere). That is an orbit.
 |
| Cannonball fired at 7.3 km/s |
Because the acceleration due to gravity falls with distance, the
velocity necessary for such an orbit decreases with greater radius from the
center of the planet. Near the planet’s surface the velocity can be quite high;
orbital velocity just above Earth’s atmosphere is about 7.8 kilometers/second.
This gives an object there an orbital period of 88 minutes. At greater orbital
radii the orbital velocity drops and the length of the orbital path increases,
leading to greater orbital periods. At some orbital radius—42,164 kilometers
for Earth, which is an altitude of 35,786 km above the equator—the orbital
period will match the rotational period of the surface, meaning the orbiting
object will not appear to move west or east in the sky (though it may move
north or south unless it orbits directly above the equator; all orbits pass
over the equator). This is a geosynchronous
orbit.
Returning to our thought experiment, consider what happens if we
increase the initial velocity even more. Now the cannonball gains altitude as
it travels. However, moving away from the planet requires the cannonball to
lose kinetic energy—put another way, the rate at which the “down” direction is
changing slows as the cannonball gets further from the planet, so centrifugal
acceleration decreases until it falls below gravitational acceleration—and the
upward velocity falls. At the exact opposite side of its orbit, across the
planet from the cannon, the cannonball has lost so much velocity that it stops
rising and instead starts falling back towards the planet. But in doing so it
gains energy back, and after one more half-orbit it returns to the position of
the cannon with the exact same velocity it started with.
 |
| Cannonball fired at 8 km/s |
So this is still an orbit, with all energy ultimately conserved, but
rather than a circle the path of the cannonball marks out an ellipse, with the center of the planet
located at one of the foci.
Kepler’s laws describe the motion of objects on these elliptical paths, and I'll refer to them from time to time, but
for now just remember that so long as we are only dealing with 2 bodies that are interacting only through gravity, with no additional forces acting on them, there are a few rules that apply to all elliptical orbits:
- The object orbits within a plane that passes
through the center of the parent body.
- The object follows the same path with every orbit,
and always takes the same amount of time.
- The object moves fastest at closest approach to the
parent body and slowest when furthest away.
If any additional forces do act on the object, this
will always change its orbital path, but the path will only continue to change so long as the force is acting. After the force stops, the object will continue on a new orbital path, which will necessarily return it back to the point where that force stopped acting on it.
Altogether, this means that an object in orbit is not in some fine equilibrium that it can easily be knocked out of; the velocity can change significantly and still leave the object in a perfectly stable orbit.
(I'm assuming here that we're
mostly dealing with a very small body orbiting a much more massive body, but
really these rules still apply for 2 similar-mass bodies, just with the
added complication that both bodies are moving on their own elliptical
paths that will have the same shape but may be different sizes depending
on their mass ratio.)
 |
Circular orbits for 2 objects with decreasing mass ratio from left to right (top) and an elliptical orbit for 2 equal-mass objects (bottom). Zhatt, Wikimedia
|
Before we move on, there is one more trajectory the cannonball can have
besides circular and elliptical. As we keep increasing the initial velocity,
the elliptical path becomes ever more stretched out, and the period required
for the cannonball to complete one orbit ever longer. As the cannonball gets
further from the planet, gravity becomes weaker, and it takes longer to
accelerate the cannonball back towards the planet. Eventually the initial
velocity is great enough that the cannonball leaves the planet so quickly that,
even given infinite time, gravity can never completely stop the cannonball. In
fact, the gravity can never remove more than a finite amount of the cannonball’s
velocity. The cannonball never returns, and so follows a hyperbolic trajectory.
 |
Cannonball fired at 11.2 km/s. In this case it is moving at exactly escape velocity and so follows a parabolic path; realistically we would expect an escaping object to follow a hyperbolic path that becomes nearly straight as it recedes from the planet.
|
The velocity required to achieve this is termed escape velocity, and though it depends on the total mass of the
system and distance between bodies, it is independent of direction (so
long as that direction doesn’t cause the bodies to collide). Even if a
satellite starts with an escape velocity towards the parent, it will pick up
enough speed as it falls to shoot back out and escape. In reality, if we have
an object on a hyperbolic trajectory escaping from Earth, it will soon deviate
from that trajectory and enter an elliptical orbit of the sun.
The escape velocity is also the velocity an object starting at rest at a great distance from the planet will be accelerated to as it approaches the planet (technically it would have to be an infinite distance, but in a realistic scenario we can assume that any such object always has some initial velocity). This means that an object approaching the planet from afar will necessarily shoot past it and escape again unless some other force acts to slow it down (e.g. air resistance, a rocket firing, collision with the planet, or interaction with a 3rd body).
(One more caveat: very compact, massive bodies like black holes will break many of these rules due to the effects of general relativity, causing orbiting bodies to spiral in towards them and capturing passing objects into orbit without the need for an additional force. Technically all orbiting bodies gradually spiral into each other and will eventually collide if given enough time, but for a typical case like a planet orbiting a star, it would take something like quadrillions of years for their orbital paths to significantly change this way.)
To save you all some time, here are the equations for the velocity
necessary for a circular orbit and escape for given radii and system mass. If
you set the altitude near the surface of a body, these should roughly tell you
the delta-v needed for a spacecraft to reach orbit and escape that body (I’ll
explain delta-v and other aspects of spacecraft navigation another time, but
probably not for a while; for now I refer you to Atomic Rockets). Note in both
cases that if a satellite is much less massive than a parent body, the parent
body’s mass can be used for the system’s mass and the satellite’s altitude plus
the radius of the parent body can be used for the radius of the orbit.
v = orbital
velocity (meters/second)
G = gravitational
constant; 6.67408*10-11 m3 kg-1 s-2
M = total mass of
the system (kilograms)
r = radius from the
barycenter (meters)
(unlike escape velocity this is not independent of direction, and must
be perpendicular to the direction to the barycenter)

ve = escape
velocity (m/s)
otherwise as above
(so it’s about 1.41 times the circular orbit velocity)
Orbital Elements
The size and shape of an elliptical orbit can be described with two
values:
Semi-Major
Axis (a): Half the length of the
ellipse on its longest axis. For a circular orbit, this is the distance between
the center of the two bodies. When people say orbital distance, radius,
or separation, they are generally
referring to this value. Per Kepler's 3rd law, this value is directly proportional to the orbital period, like so (also incorporating Newton's law of gravitation):
P = orbital period
(seconds)
a = semimajor axis
(meters)
G = gravitational
constant; 6.67408*10-11 m3 kg-1 s-2
M, m = mass of the two bodies (kg)
But as I've mentioned before, you can make this calculation far simpler by using the right units. For example, if you want to know the orbit of a planet around a star, you can describe mass and period in relation to Earth's orbit around the sun (eliminating the constants, as these units are already related by these laws) and assume the planet's mass is negligible compared to the star's (eliminating the need to account for the planet's mass, as only the total mass is important), you can determine orbital period like so:
P = orbital period
(years)
a = semimajor axis
(AU)
M = mass of the star (relative to sun's mass)
Eccentricity (e): A measure of how elongated the orbit
is. e = 0 is a circular orbit, 0 <
e < 1 is an elliptical orbit that
is more elongated for higher values of e,
e = 1 exactly is a parabola but
realistically never occurs, and e >
1 is a hyperbolic escape trajectory. More precisely:
ra = greatest
separation between bodies
rp = least
separation between bodies
From these values we can define two important points in the orbit:
Apoapsis (ra): The point of greatest
separation. Also refers to the distance between the bodies at that point.
A.K.A. apocenter, apogee (for orbits around earth), aphelion (for orbits around the sun), apastron (for orbits around any star).
Pretty much every major solar system body has its own term that is rarely used (perhaps we should use "apotea").
ra = a (1 + e)
Periapsis (rp): The point of least
separation, or distance at that point. Has all the same variations as above. rp = a (1 – e)
One more value helps us understand the orientation of an orbit relative
to the parent body:
Inclination (i): The angle between the plane of the
orbit and a reference plane. For orbits around planets and similar bodies this
reference is the equatorial plane of
the planet, but for orbits around the sun we tend to use the ecliptic, the plane of the Earth’s
orbit (so-called because the moon passes through it during eclipses) even
though this is inclined from the sun’s equator by 7.25°.
For orbits around the
Earth (or any other similar body), the inclination has some implications for how the object moves over the surface:
- At i = 0° an object remains
permanently over the equator and moves east over the surface, such that when
viewed from above the north pole it is moving counterclockwise around the
planet; this is referred to as prograde
motion (actually this is only true for orbits below geosynchronous orbit; higher-orbiting objects will appear to move west as their orbital motion lags behind the surface's rotation, but are still classified as moving prograde).
- At a value between 0° and 90°, say i = 60°, the object still
moves west but also oscillates north and south until it is over points at 60°
north or south latitude (that is, directly overhead from the ground's perspective, so a high-orbiting
satellite can be above the night side and still see over the Earth to the sun). If there is no simple fraction between the object's orbital period and the planet's rotational period, it will eventually pass over every point of the surface between those latitudes.
- At i = 90°, the object passes
directly over the poles. If, again, there's no simple orbit/surface rotation ratio, it will eventually pass over
every point on the surface.
- At i >
90°, the object will move west over the surface, and is said to be in a retrograde orbit (in this case, regardless if it's above or below geosynchronous orbit). Otherwise they’re similar to orbits
with inclinations equal to 180° - i,
though once you take the other elements into account they’re orientated
differently.
- At i = 180°, the maximum,
an object orbits west over the equator.
We can now define two more important points in the orbit:
Ascending node: The point where
the object passes through the reference plane heading “up”; i.e., where it
passes over the equator heading from the southern hemisphere to the northern
hemisphere.
Descending node: As above, but
heading “down”, from north to south.
This tells you most of what you need about any given orbit. If you’re
told these elements—semi-major axis, eccentricity, inclination—for a planet in
a given star system, you can reasonably ballpark its habitability, surface
climate, and likelihood of encountering other bodies. But if you want to know
exactly how an orbit is orientated, such that you can compare it to other
nearby orbits, you need two more values:
Longitude of the
ascending node (Ω): The angle between a
reference direction (within the plane of the reference plane used to measure
inclination) and a line connecting the barycenter to the ascending node, measured
counterclockwise from the reference (as viewed from “above”). The standard
reference direction in the solar system is towards the First Point of Aries, which is the same as the direction the sun
appears from Earth during the vernal equinox (or it was when this system was defined). A.K.A right ascension of the ascending node, or RAAN, when used with this
reference. For an orbit with i = 0°,
the position of the ascending node is undefined, but by convention this is set
to Ω = 0°.
Argument of
periapsis (ω): The angle from the
ascending node to the periapsis, moving in the direction of the objects motion,
and within the plane of the orbit, not the reference plane. Has all the same
name variations as periapsis.
This all tells us the shape and orientation of the orbital path, but if
we want to know the position of an object within this path, we need one more
value:
True anomaly (ν, θ,
or f): The angle from the periapsis
to the object’s position, along its direction of motion. Often we define a
reference time, called the epoch,
and then define the “true anomaly at
epoch”, allowing the object’s position to be calculated for any other time.
This works even if the object wasn’t in its current orbit at epoch, because we
can just extrapolate the current orbit backwards. By convention astronomers use
a common epoch called J2000,
corresponding to 12:00:00 midnight on January 1, 2000 on the Gregorian
Calendar. Some people will use mean
anomaly instead, which is similar but not the same (it’s the angle to where
the object would be in a circular but otherwise identical orbit—thus it changes
at a constant rate). They can be converted into each other, but it’s annoying math I won’t reproduce here.
These 6 elements can define any 2-body orbit, and indeed no such orbit
can be defined with less than 6 values. So if we want to construct a planetary
system that can be loaded into simulations, we have to define these elements
for every body within that system, along with their masses. Other
characteristics of these bodies—radius, composition, etc.—can all be left for
later if we desire.
When discussing a planet, however, it may also be convenient to know how the planet's rotation relates to its orbital motion. We can describe this with two more elements:
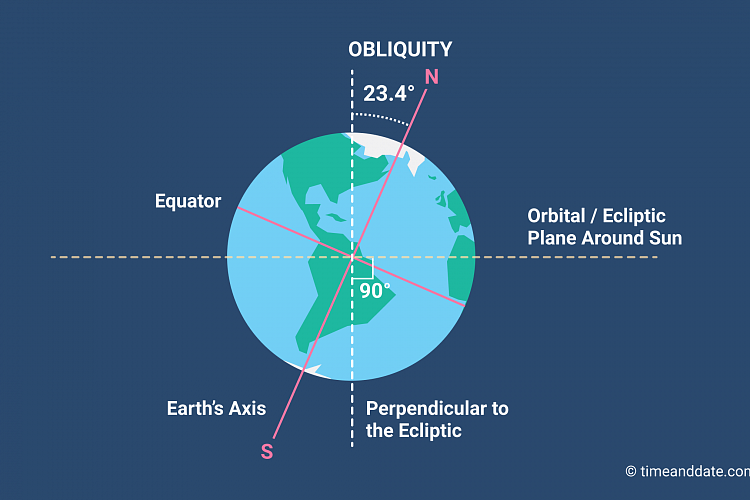
Obliquity (ε): The angle between the object’s
equatorial plane and the plane of the orbit, A.K.A axial tilt. As with inclination, there’s a convention regarding
direction of spin, whereby an object with ε
< 90° spins in the same direction as it orbits and is said to have prograde
rotation (actually some people will define it relative to the direction most of the system orbits, regardless of which direction the object itself orbits, but for consistency I'll stick with the former definition) and an object with ε >
90° spins in the reverse direction and is said to rotate retrograde.
Argument of
obliquity: The angle between a line from the object’s center to the center of its
orbit (i.e. the star) at periapsis and the direction from the object’s center
to the north pole within the orbital plane (so changing the obliquity to any
nonzero value shouldn’t change this value) measured counterclockwise as viewed
from above (in the direction of rotation for a prograde-rotating planet). If
this value is 0, summer solstice in the northern hemisphere coincides with the
periapsis; for greater values it will occur later in the year, like so:
- 0°: Periapsis coincides with northern summer solstice.
- 90°: Periapsis coincides with northern fall equinox.
- 180°: Periapsis coincides with northern winter solstice.
- 270°: Periapsis coincides with northern spring equinox.
This is only one
of several conventions for describing an object’s rotational axis, but it’s the
most convenient for use in this blog.
n-Body Motion
All the discussion we've had so far applies to 2-body systems; systems where there are two bodies (two stars, a planet and a star, a satellite and a planet) attracted to each other by gravity, with no significant outside influence. These systems obey Kepler's laws, and so are essentially unchanging; the bodies will move in the same orbital paths, always with the same period, for as good as forever (until the effects of general relativity become significant, anyway), and so with a few equations we can see the system as it exists today and predict how it will look at any point in the future.
However, in many cases there will be more than two bodies present. Unfortunately, even a 3-body system no longer behaves with such perfect predictability. Systems of 3 or more massive bodies all attracted to each other are chaotic; a tiny change in the initial state of the system can lead to huge changes in the future. They do still obey Newton's laws of motion, so we can measure the current state and try to simulate how they will develop in the future, but because we can never measure reality perfectly, even in principle, our simulations will always diverge from reality eventually (though depending on what factors we're simulating, this can take billions of years). These simulations also require a lot more computing power than simply working through Kepler's laws for a 2-body system.
Fortunately, if we leave any such n-body system ("n" being the number of massive bodies) to its own devices, it usually won't take long for one of two things to happen:
- One of the bodies is accelerated to such high velocity that it leaves the system and no longer exerts a significant force on the remaining bodies.
- The bodies will eventually organize themselves into a hierarchy, such as a star-planet-moon system; the planet-moon distance is so small compared to the star-planet distance that the planet and moon experience basically the same acceleration from the star (and thus, negligible acceleration relative to each other) and the star experiences the pull from the planet and moon as effectively a single force towards their barycenter.
In the first case, we may eventually be left with just 2 bodies remaining, simplifying matters. But in the latter case, the hierarchy allows us to approximate the planet and moon as a 2-body system to describe their motion relative to each other, and then treat them as a single body so that we can approximate them and the star as another 2-body system. These approximations tend to do a fairly good job of describing the behavior of hierarchal systems even for fairly long periods, at least on a qualitative level (semimajor axis tends to the most stable element, eccentricity and inclination less so and the others even less, and objects further down the hierarchy (i.e., moons) or with shorter orbital periods tend to have less stable orbital elements overall).
Within such a hierarchy, we can define a region for each body (other than the most massive body), called the Hill sphere, where it's gravity is strong enough relative to its "parent" (the body it directly orbits) such that a small object in that region will tend to orbit around that body, rather than following an independent orbit around the parent. The radius of this spherical region can be approximated like so, for a body on a near-circular orbit with a low mass compared to its parent:

RH = Hill radius (any unit so long as a uses the same)
a = semi-major axis
m = mass of the
orbiting body (any unit so long as M uses the same)
M = mass of the
parent body
If a small body lies within a planet's Hill sphere, we can approximate the motion of that body as an elliptical or hyperbolic orbit around the planet, and then assume that 2-body system moves around the planet's star in turn; and we can do much the same with a body in the Hill sphere of a moon that orbits both the planet and the star alongside the planet (this is often called the "patched conics" approach). In reality, objects near the outer edge of a Hill sphere tend to deviate from these approximations, but they tend to work well enough for objects in more stable orbits.
 |
Nested Hill spheres of the Sun, Earth, and Moon; the sun's "parent" for these purposes is the rest of the galaxy, and I'll explain Roche limits in the next post. Cmglee, Wikimedia
|
But there are a few other ways that 3-body (and occasionally other n-body) systems might obtain stable, predictable motion without a hierarchy. Many of these solutions are intriguing but require absurdly specific starting conditions or would quickly fall apart if even slightly perturbed by an outside force, and so we wouldn't expect to see them occur naturally.
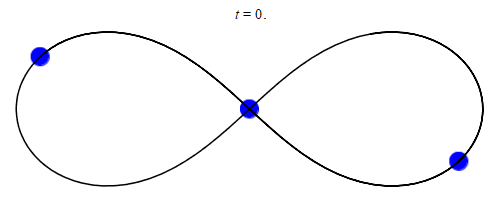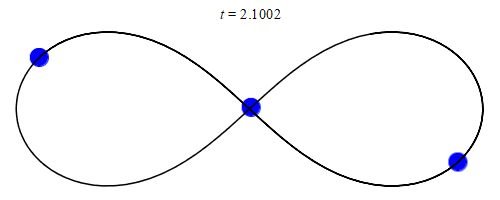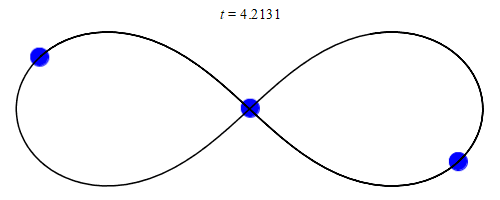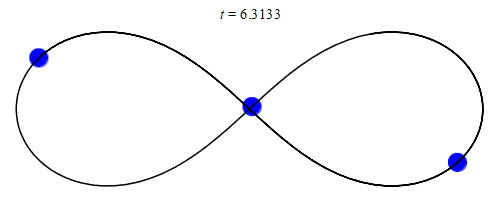 |
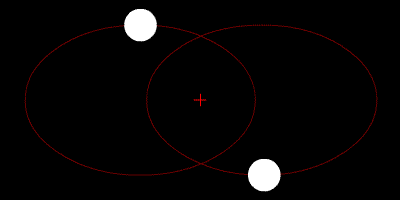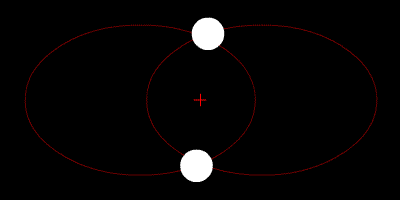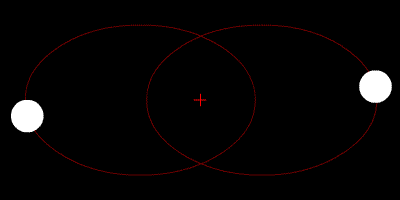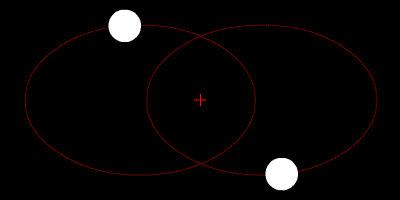
A figure-8 orbit between 3 equal-mass bodies. This solution can actually tolerate small changes in mass or external perturbations and so might occur naturally2, but a figure-8 trinary star system is likely no more common than 1 per galaxy even on the optimistic end. MaxwellMolecule, Wikimedia
|
But a fairly common 3-body system that I've mentioned before is a body at a Lagrange point. For a 2-body system where a low-mass body like a planet orbits with reasonably low eccentricity around a more massive body like a star (a moon around a planet or a star around a more massive star works as well), there are 5 points where an additional body could be placed and, under the combined influence of the star and planet, orbit the star with the same orbital period of the planet such that it doesn't appear to move relative to the planet:
- L1: Directly between the star and planet, closer to the planet(approximately at the edge of the Hill sphere); the planet's gravity counteracts the star's gravity, and so the object behaves as if the star has a lower mass and so orbits slower than it would otherwise at that distance.
- L2: Directly on the other side of the planet from the star, slightly further from the planet than L1; the planet's gravity adds to the star's, and so the object behaves as if the star has a higher mass and so orbits faster than it would otherwise at that distance.
- L3: Directly on the other side of the star from the planet, slightly further from the star than the planet is; again, the combined gravity of the star and planet causes it to orbit slightly faster than it would otherwise, but because the planet is further away, the effect is less dramatic than for L2.
- L4: In the same orbital path as planet, but 1/6 of an orbit ahead such that it is at the same distance from the star and planet; here the gravity of the sun and planet is balanced such that the object always accelerates directly towards their barycenter, whereas objects elsewhere in the planet's orbit will accelerate elsewhere and so follow slightly different orbital paths.
- L5: The same as L4, but 1/6 of an orbit behind the planet
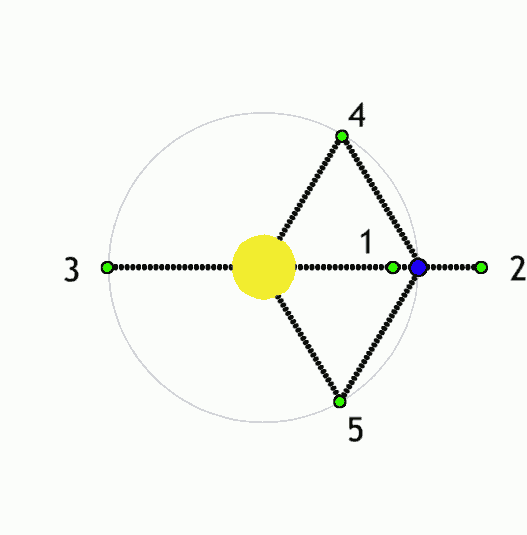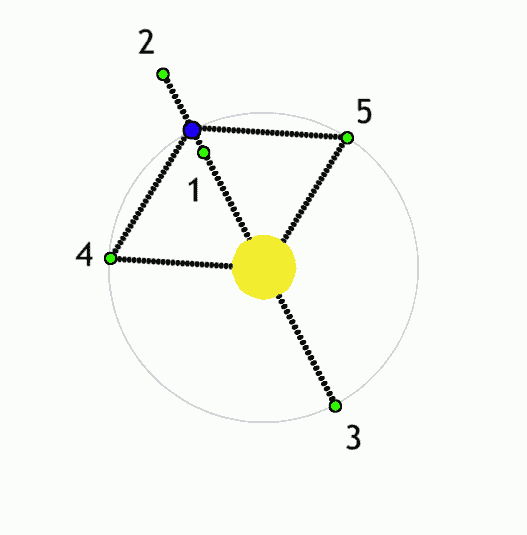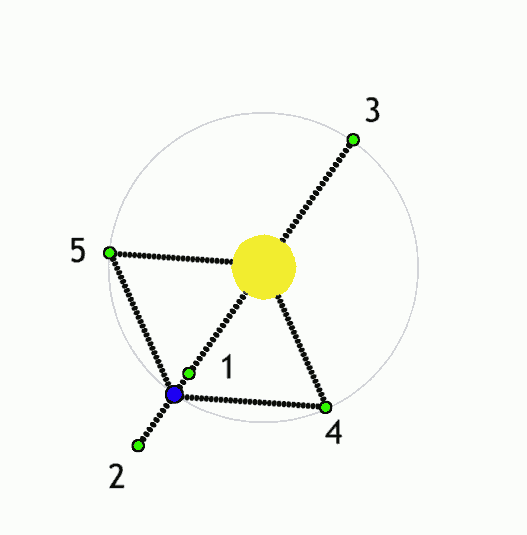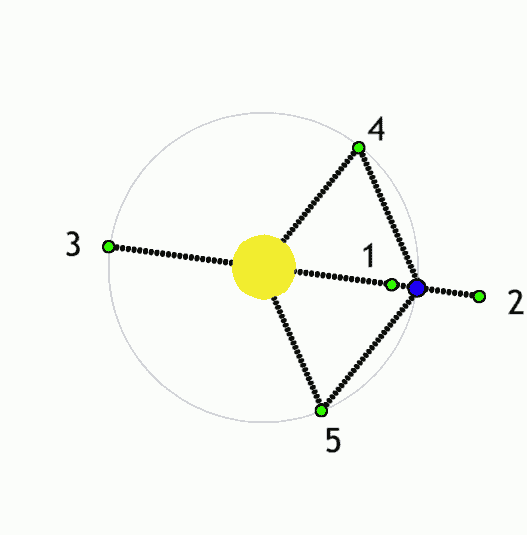 |
Lagrance points (green) for a system with a lower-mass object (blue) orbiting a higher-mass object (yellow). Anynobody, Wikimedia
|
L1, L2, and L3 are all only quasi-stable; an object placed exactly there with no additional influences will stay there, but even a small perturbation from a 4th body (another star, planet, or moon, or even a passing asteroid) will cause it to drift away and eventually enter a new orbit of either the planet or star. As such, we shouldn't expect to see natural bodies appear there for more than brief periods.An object placed at L4 or L5 (called a trojan) will also drift out of position when perturbed, but rather than leaving for an entirely new orbit, the combined influence of the planet and star will cause it to oscillate around the Lagrange point, moving in a tadpole-like pattern relative to the planet (there are some similar oscillating motions possible around the other Lagrange points that can extend the lifetime of objects there, but none are stable in the long term). This motion could conceivably be small enough as to be negligible for anything but precision engineering, or large enough that the distant between the object and the star or planet varies considerably across multiple orbits of the star.
We'll talk about trojans and other co-orbiting bodies more in the next post; for now, note that these systems could plausibly remain stable for billions of years so long as3 the star is at least 24.96 times the mass of the planet. There seems to be a common misconception that the planet need be significantly more massive than the trojan, but so far as I'm aware no such restriction4 has been found; "mutual trojans" of equal mass orbiting a larger star appear to be stable (though I'm unclear if the 24.96 minimum mass ratio with the star applies to each body or their combined mass), and even systems of 3 or more equal-mass trojans have been suggested5.
That about wraps it up. I know there's not a lot of interesting worldbuilding to talk about this time, but if you're confused about any of the terms or concepts regarding orbits in later posts, you can refer back here. The next post in particular involves a lot of discussion regarding the orbital motions of planets within star systems.
1 "What are the kinematic formulas?", Khan Academy
2 Montgomery, R. (2001). A new solution to the three-body problem. differential equations, 1001, d2xi.
3 "The Lagrange Points", Document Created by Neil J. Cornish for WMAP Education and Outreach/ 1998
4 Kemp, S. P. (2015). An examination of the mass limit for stability at the triangular lagrange points for a three-body system and a special case of the four-body problem. San José State University.
5 Salo, H., & Yoder, C. F. (1988). The dynamics of coorbital satellite systems. Astronomy and Astrophysics, 205, 309-327.
Previous Versions:

















Comments
Post a Comment