An Apple Pie From Scratch, Part II: Stars

Concept of AR Scorpii system. M. Garlick/University of Warwick/ESO

If we want life, we’re going to need a habitable world. It’s possible some simple life could exist on a rogue planet separated from all stars, but we’re aiming a bit higher than simple life. If we want complex, intelligent life then we need a plentiful, reliable energy source, and on that count it’s hard to do better than sunlight. So we’ll need a star, and many aspects of life on our habitable world will be determined by the type of star we choose.

Star Types

Though the variety of star types may seem daunting at first, really almost all variation among stars comes down to mass and age. A star with a given starting mass will predictably “evolve” through major stages as it ages, and many important characteristics of stars are directly related to mass. There are some variations due to composition, but for the most part they’re too subtle to be worth bothering with here.

When astronomers observe stars, they classify them by luminosity, their total light output, and effective temperature, the average temperature of the visible surface, which determines their color (roughly¹). A Hertzsprung-Russel (H-R) diagram charts stars by these two values, and shows clearly that the vast majority can be grouped together in a prominent diagonal strip. This is the main sequence, where stars spend the majority of their matter-fusing lives, and it accounts for around 90% of stars in the galaxy today. The lightest main sequence stars are at the bottom right and the most massive are at the top left, with a consistent mass gradient between them. That is to say, massive stars are bright, blue, and hot, and lighter stars are dim, red, and cold.

Richard Powell, Wikimedia

“Cold” being a relative term; the coldest luminous stars are still over 2400 Kelvin, but the very hottest push past 50,000 K. Many people tend to exaggerate the color difference; incandescent light bulbs have a similar temperature to the coldest main sequence stars, and so put out a similar spectrum of light, and candles are even colder. The range of colors seen on a planet orbiting one of these cold stars would be noticeably shifted towards orange, but not uniformly blood red as is sometimes depicted—and human color perception tends to adjust to ambient conditions anyway. The hottest stars can be quite blue, but as we’ll see in a moment we don’t need to worry much about the conditions of planets orbiting them.

Kieff, Wikimedia

In order from bluest and hottest to coldest, these stars are grouped into the spectral types O, B, A, F, G, K, and M (yeah, it’s a weird sequence, they didn’t know the proper order when they started naming spectral types) with divisions at roughly 30,000, 10,000, 7500, 6000, 5200, and 3700 K. Each type is subdivided by appending a number from 0 to 9, again in order from hot to cold—you will also sometimes hear researchers refer to “early” or “late” members of a type, in the same order as these numbers. The sun is a G2 star, comfortably in the middle, with an effective temperature of around 5778 K.

But stars don’t sit still. Very young stars are still contracting under gravity, and the extra energy causes them to start briefly brighter and then “descend” onto the main sequence, moving down on the H-R diagram as they get dimmer and generally a bit hotter.

Blue numbers are masses in solar masses of stars moving along the blue tracks, red numbers are ages of stars as they pass the red isochrones (lines of equal age). Stahler and Palla 2008

On the main sequence, helium builds up in their cores and causes the cores to contract and grow hotter over time, pushing the outer layers out; the overall effect is to make stars brighter and slightly hotter as they age, shifting them a bit up and left on the H-R diagram. Once they run out of hydrogen fuel, they leave the main sequence and evolve through various post-MS stages. Generally this will push them towards the upper right corner of the H-R diagram, though stars of different masses can pass through a lot of odd detours.

Post-MS evolution of a solar-mass star. Penn State Astronomy & Astrophysics

These dying stars can pass through several spectral types as they age, so to distinguish them from the main sequence astronomers also group stars into classes in order of decreasing luminosity (though there’s some luminosity overlap; they only appear distinct on the H-R diagram). Classes 0, Ia, Ib, II, III, and IV are all varieties of post-MS stars, collectively called “giants” because they’re much larger than their MS predecessors. Class V is main sequence stars, which are also called “dwarfs” even though the largest O-type dwarfs can be larger than some giants. Class VI is a subset of MS stars, called “subdwarfs” that are particularly metal-poor and so dimmer than similar-mass class V stars. Class VII, at the lower right corner of the H-R diagram, includes white dwarfs, the final evolutionary stage for many stars once fusion in the core stops entirely.

Spacepotato, Wikimedia

Though many stars share similar evolutionary stages, the timing of stages can vary widely between stars, again based on mass. As I mentioned in the last post, more massive stars live dramatically shorter lives. Even though they have a larger fuel supply, the greater pressure within their cores causes them to burn through their fuel much faster. Additionally, more massive stars have poorer internal convection, so their cores will run out of fuel even while there’s abundant hydrogen in the outer layers. Large stars can die² even while over 4/5 of their mass remains hydrogen.

If we want a planet to have time to develop intelligent life, we’d better be sure its star lasts long enough. The most massive O-type stars live a scant few million years; too short to finish forming planets, let alone develop life. If we want a star to last for at least 1 billion years to give life a good chance to appear, the most massive it can get is about 2.2 solar masses (1 solar mass = the mass of the sun), a large A-type star. For a lifetime of at least 4 billion years, about the time for complex life to emerge on Earth, we have to limit ourselves to F-type stars under 1.4 solar masses.

But the window of opportunity for life to appear on a planet is not always the same as the star’s lifetime. As stars brighten with age, the habitable zone (HZ)—the range of orbital distances where a planet can have stable liquid water on the surface—moves outward. Excepting an especially fortuitous case of planetary migration, a single planet can only remain within this zone for so long. The presence of life on a world may actually help increase this habitable period³, but only to an extent.

Source

So even though the sun has another 6 billion years of life left in it, within 1 or 2 billion years the Earth’s atmosphere will be stripped away, the oceans boiled off, and the planet left a lifeless husk. Because larger stars have larger habitable zones, the maximum habitable time is a larger proportion of their total lifetime, but to get a habitable time comparable to the current lifetime of Earth, our limit is a midrange F-type star⁴ with 1.2 solar masses. Fortunately, the longer lifetimes of lighter stars also makes them more common (they also form more often today), meaning that roughly 98% of main sequence stars in the galaxy today are below this mass limit.

Now that we’ve situated ourselves within the range of star types, let’s explore the differences between stars of different masses and how hospitable they may be to life. Note that I’ve chosen these categories more to reflect post-MS evolution than main sequence habitability, though I’ll discuss that as well.

0.08-0.25 Solar Masses; Late M

Concept of GJ1214. ESO/L. Calçada

We’ll start our tour with the lightest main-sequence stars, the red dwarfs. These stars have low rates of fusion and good convection throughout their interiors that keeps their cores supplied with hydrogen, allowing them to remain on the main sequence for 1 to 12 trillion years. They’re also very common, accounting for 41% of nearby main sequence stars.

Because these stars evolve so slowly, a planet can remain in the HZ for a very long time, plenty long enough to develop complex life. The dim light output does mean they will have smaller, thinner HZs, reducing the chance of a planet forming in this zone, but they’re also more likely to form planets at smaller orbital radii anyway and observational evidence⁵ indicates they have a higher proportion of small, rocky planets compared to larger stars.

Long life doesn’t guarantee habitability, though. A longer main sequence stage also comes with a longer pre-main sequence bright period that, for the smallest stars, could last billions of years⁶. During this stage they have both higher luminosity and an increased rate of flares that produce X-rays and ultraviolet radiation (XUV), and charged particles. A planet at the correct radius for habitability in the main stage of the star’s life would first be blasted by intense light and energetic radiation at this early stage that could strip its atmosphere away. Even if the atmosphere survives, large quantities of water may evaporate and rise to the upper stratosphere, where photolysis, a sunlight-driven chemical reaction, will split it into hydrogen, which escapes into space, and oxygen, which builds up in the atmosphere⁷ (which is why, when we have telescopes good enough to identify the composition of exoplanet atmospheres, we shouldn’t immediately assume that oxygen means life).

Pre-MS evolution of various stars; red dots are start of the main sequence, "Gyr" is billions of years. Ramirez and Kaltenegger 2014

But recent modelling has shown that it may be possible for a world with an initial water content similar to Earth to survive with a significant portion remaining⁸, let alone waterworlds with many times Earth's water. Indeed, the planets in the TRAPPIST-1 system, orbiting in or near the HZ of an M8 star, have densities consistent with high water content⁹ (these initial estimates have since been somewhat amended down¹⁰, which actually improves habitability in this case). Even if the surface is totally dried out, water stored in the mantle¹¹ could later emerge onto the surface through volcanic activity.

Planets could also migrate inwards after the star had matured past its rebellious phase, but they’d have to pass through a period of high eccentricity (variation in distance from the star throughout an orbit) during which they’d experience intense tidal heating that would leave them charred and dry¹²; this could be a threat even to planets with lower eccentricity in the HZ. Another intriguing possibility¹³ is that mini-Neptunes could form and then migrate into the future HZ, where they would then lose their thick Hydrogen/Helium atmospheres to leave rocky, habitable cores.

But even if the atmosphere survives, the harsh XUV radiation from frequent flares may be an issue for early life. It could cause harsh surface radiation¹⁴ for planets without enough atmospheric oxygen to form an ozone layer, though as mentioned it may also cause oxygen to form; but the oxygen itself could block some chemical pathways that may have been vital to the development of early life (this may sound odd to our oxygen-breathing sensibilities, but oxygen is useful to us because it's so volatile; think of it as the difference between learning to use gasoline to power a car as an adult, and tossing burning gasoline onto an infant).

But it may be that the strong magnetic fields that cause these large flares also direct them mostly out from the star's poles¹⁵; most should completely miss planets orbiting over the equator (as planets usually do). Besides, most of the harmful radiation¹⁶ likely occurs in the first billion years of the star's life—it's not even clear if Earth had life for most of its first billion years.

Once the star quiets down, radiation in the HZ may actually become too low¹⁷, reducing the surface production of organic molecules necessary for life. But presumably there’s an intermediate stage of ideal conditions in there, and any life that forms before then could survive underground or in the deep ocean. Even if life doesn’t appear until the end of the star’s active stage, a delay of a few billion years is insignificant next to a habitable era tens or hundreds of billions of years long.

Visible light too is lower in the HZ, and shifted towards lower-energy red wavelengths, but it should still be sufficient¹⁸ to support photosynthesis. Some authors have speculated that plant life in a red dwarf system should develop to absorb as much of the little visible light as possible, so it may appear black to human eyes (The exact mechanics behind why plant life on Earth uses the spectrum of light it does is a bit complicated, so I’ll tackle it in more depth in a later post regarding biochemistry).

Tidal-Locked Planets

Even if a planet survives past the early bright period, a further danger comes from tidal forces. Just as the moon’s gravity causes tides on Earth, the sun causes tides as well; the sun’s gravity is stronger on the day side of the planet than near its center, so a bulge of gas, water, and even rock forms on the point facing the sun; similarly, the sun’s gravity is weaker on the night side of the planet than near the center, so a second bulge is formed on the point furthest from the sun of material “left behind” as the planet is accelerated towards the sun. As the planet rotates it moves these bulges out of position, but the sun’s gravity drags them back, producing internal friction that both heats the planet and slows its rotation.

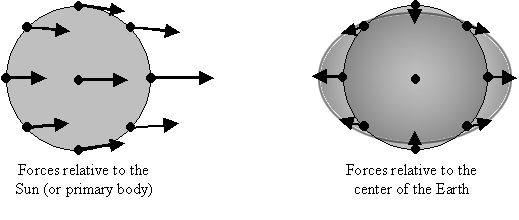
Source

For the Earth, tidal forces from the sun aren’t too important. The moon’s influence is stronger, and has slowed Earth’s rotation—lengthening the day from 4 to 24 hours. But a planet orbiting in the HZ of an M-type star will experience much greater tidal forces from the star. It’s likely that shortly after formation most such planets will be tidal-locked to their star, causing them to enter synchronous rotation; their day is exactly as long as their year, meaning that one side—the dayside—permanently faces the star and the other side—the nightside—is in eternal darkness. This eliminates most tidal friction, though axial tilt (obliquity) and change in orbital distance (eccentricity) can still cause some, and will tend to be dampened over time as well. Given enough time and no competing influences, tidal forces will lock a planet into a perfectly circular orbit with no obliquity, and both the substellar point—the point in the middle of the dayside directly facing the star—and the terminator—the line dividing the dayside and nightside—standing completely stationary on the surface.

Beau. TheConsortium, Rare Earth Wiki

We used to think that this was the end of the story, with the nightside locking away any but the thickest atmospheres in ice and the dayside left a barren landscape by intense sunlight—leaving, at best, a thin, barely habitable twilight zone constantly wracked by intense winds. But once again, recent modelling has been more optimistic. Atmospheric and ocean circulation¹⁹ should keep the nightside above 240 K on average and limit ice formation²⁰ to a ~10 m layer over water and ~1 km layer over continents even with much thinner atmospheres and smaller oceans compared to Earth. This means the distribution of continents on the nightside could alter sea level on the dayside, but is unlikely to leave it completely desiccated except on the driest worlds. On the dayside, a feedback effect of increasing cloud cover for increasing insolation (light intensity from the star on the surface) could stabilize the climate²¹, increasing both the habitable area on the surface and size of the star’s HZ.

Yang et al. 2014

For a perfectly tidal-locked world, the star would remain motionless in the sky. Shadows would be more-or-less permanent, and even in temperate or fairly warm regions there may be frozen valleys that never receive direct sunlight. Plants may experience fierce competition for access to sunlight, which may alter the sort of forest ecosystems that could develop—undergrowth may be in trouble if it’s easier for tree canopies to completely monopolize the light.

https://external-preview.redd.it/Xlq7G7wGsxQHoy-1HUBYrfZZHyGkqeRF0_tMISmJXwk.jpg?auto=webp&s=01aa433c8b2814d0656f29524fcdc0e3726782e3

Space Engine

But it’s also possible for slight imperfections in the planet’s orbit to cause the star to appear to shift slightly in the sky. Obliquity will cause the star to oscillate north and south over the course of the year, and eccentricity will cause it to oscillate east and west. This can cause strips of land to cross over between the day side and night side, and other regions will experience an odd sort of seasonality due to the sun getting higher and lower in the sky. The two effects in combination could even cause “summer” to circle around the perimeter of the day side, with “winter” on the opposite side of the planet.

Even a planet with very strong tidal forces is likely to develop these orbital imperfections if there are other planets in the system exerting a gravitational influence. But if they grow too large, the tidal heating may produce extreme volcanic activity that prevents life from developing on the surface.

Libration of the Moon from Earth's perspective. Tomruen, Wikimedia

But tidal-locking doesn’t inevitably lead to 1:1 synchronous rotation; planets with thick atmospheres could experience uneven heating that will lead to tidal effects altering their day length²². A planet with some eccentricity may also settle into²³ a 3:2 spin-orbit resonance like Mercury in our solar system, completing 3 revolutions about its axis for every 2 orbits around the star, which means that 1 solar day lasts for 2 orbital periods. For a world orbiting in the HZ of a minimum-mass red dwarf, these days can be as short as 10 Earth days—but tidal forces in the HZ are strongest for such a star, strong enough to either preclude such an orbit from forming or producing enough heat in the planet’s interior to induce extreme volcanic activity. For a world orbiting a larger star, nights would be long but could still be shorter than the seasonal nights of the poles on Earth, and with much brighter days. We can easily imagine all life on such a world developing a hibernation-boom lifecycle like we see in the taiga regions of Earth.

There are even more possible resonance states²⁴, but we'll leave further discussion of the climate and conditions of tidal-locked worlds for another time.

Blue Dwarfs

Every red dwarf in the universe today is still quite young, and none will leave the main sequence for a long time, but theoretical modelling of their interiors gives us a pretty good idea of what will happen when they do. When a small red dwarf eventually runs low on hydrogen fuel, the core contracts and warms, and the star spends several billion years as a blue dwarf, both much hotter and much brighter than before. Stars of about 0.2 solar masses and above can even become brighter than our sun is now.

For the most part this marks the end of habitable conditions for that system; planets that used to be in the HZ will be baked dry, and for most blue dwarfs the luminosity—and thus position of the HZ—changes too quickly for any other planets to be habitable for long. The one exception²⁵ is for stars close to 0.16 solar masses, which will stabilize at about 1/3 as bright as the current sun and then stay there for 5 billion years. This means that planets that had been cold, frozen, and dead for the near 3-trillion year main sequence lifetime of the star could thaw and form life, and that life could plausibly develop to the point of intelligence, all within this “short” episode at the end of the star’s life.

Evolutionary tracks of low-mass stars, starting from the middle right (spacing between the dots roughly indicates the rate of change). Adams et al. 2005

Well, some planets might do this. Ice is very reflective, so the light required to melt a frozen planet is higher than that required to keep an already-warm planet stable. Exactly how much higher depends on the spectrum of light; ice reflects less infrared than visible light. So planets melted by a main-sequence M-type star as it brightens over its lifetime could be habitable afterwards, but by the time a K, G, or F-type star—or a blue dwarf—manages to melt a planet, it will be producing enough light to immediately push that planet past habitable conditions²⁶ to something more resembling Venus. However, tidal-locked worlds are also easier to melt, and a planet orbiting a star for trillions of years will probably become tidal-locked, so habitability around a blue dwarf is still plausible.

Numbers are surface temperatures in kelvin. Yang et al. 2017

White Dwarfs

Finally, when 99% of the star’s initial hydrogen fuel has been consumed, fusion in the core ceases and the star collapses inwards until it is stopped by electron degeneracy pressure, a quantum mechanical effect that prevents electrons from being packed too closely together. The remnant white dwarf (a D-type star) retains a great deal of heat, and so continues to radiate light with gradually decreasing luminosity and effective temperature for at least 10¹⁵ years, possibly much longer depending on the nature of dark matter and proton decay. Once it has cooled to about the temperature of background radiation (which, mind you, will be much lower in the far future) it will be a black dwarf.

So even though fusion has stopped, there’s still some light to work with if we want to extend this star’s habitable period even further. Initially the white dwarf is too hot, producing intense XUV radiation, but within a few billion years it can cool enough to form a habitable zone²⁷ in an extremely close orbit (~0.01 AU) that a planet could remain within for as much as 8 billion years.

NASA/JPL-Caltech

However, we have to ask how a potentially habitable planet would end up in such a position. If it had formed there initially it would have been baked under intense light for trillions of years (or, in the case of larger stars that also form white dwarfs, swallowed during the red giant phase). A planet could migrate inwards from a safe position in the outer solar system into the habitable zone, but in doing so would have to pass through a period of high eccentricity, during which it would experience intense tidal heating²⁸ that would boil off any oceans or atmosphere and potentially even melt the surface.

Perhaps such a world could be replenished with water by later comet impacts, or a new planet could form in place after some cataclysmic event. But in such close orbits, even a tiny amount of orbital eccentricity can cause intense tidal heating. At the prime period of habitability, 5 billion years after the white dwarf forms, an eccentricity of more than 0.0001 would be sufficient²⁹ to cause a runaway greenhouse effect for planets in the HZ, rendering them uninhabitable. Venus, the least eccentric planet in our solar system, has an eccentricity of 0.0068. In a small, tight system, any other planets would likely induce eccentricities greater than this even as extreme tidal forces were working to reduce them.

Perhaps it could be possible for a combination of tidal heating and light to warm a planet outside the traditional habitable zone to liquid water temperatures, but for reasons we’ll explore in later posts this is less likely to maintain a stable climate in the long term. It’s also worth noting that tidal effects tend to push close-orbiting planets outwards—as our Moon is moving outwards from the Earth—contrary to the inward movement of the habitable zone.

So an intelligent spacefaring civilization could potentially find some use for the light from a white dwarf, but it’s unlikely to do less advanced life much good.

0.25-0.8 Solar Masses; Early M to K

Concept of Kepler-444. NASA/JPL-Caltech/AMES/Univ. of Birmingham

The next group includes more red dwarfs as well as orange dwarfs, with MS lifetimes ranging from 20 billion to 1 trillion years. They’re another large group including about 47% of nearby stars, 3/4 of which are M-types below 0.45 solar masses.

In terms of main sequence habitability, the low end of this group in terms of mass has much the same challenges as the previous one, and the high end is similar to the sun and probably just about as habitable. Some scholars consider K-type stars the ideal for life, as they have longer lifetimes than the sun and so provide longer habitable periods for their planets, but are still large enough to avoid many of the drawbacks of M-type stars.

Red Giants

What unites this group is their post-MS evolution. Similar to late M-types, none of these stars have yet left the main sequence, but when they do they’re expected to follow much the same evolutionary path as the sun and similar stars up to 8 solar masses. Unlike the previous group, interior convection is poorer and the core may exhaust its hydrogen fuel while some hydrogen remains in the outer layers of the star. When this happens, the interior contracts and temperature rises until fusion of hydrogen begins in a shell around the core. As the mass of the core increases with the products from this reaction, pressure in the shell builds and the rate of fusion increases, pushing the outer layers of the star outward and causing the star to become bigger, brighter, and redder. This is the red giant phase of stellar evolution.

Concept of Antares. ESO/M. Kornmesser

As a star develops into a red giant, the habitable zone sweeps outward through the solar system at an increasing speed, so a planet around a sunlike star with an orbital radius of 2 astronomical units (AU, the average distance between the Earth and sun) could expect to remain in the habitable zone³⁰ for over 3.5 billion years across the late main sequence and red giant stages, whereas one 3 AU out would only have 250 million years. As always, smaller stars develop slower and provide longer habitable periods³¹, as much as 9 billion years for an ideally-placed planet after the red giant stage begins for an M1 star.

If life had already developed on a planet closer to the star earlier in the system’s history, it may be possible for it to be carried to other bodies in the outer system by meteorites, giving these planets a head-start once they enter the habitable zone—or they could have developed their own life in a subsurface ocean—but below a billion years or so of habitability it’s doubtful that any could proceed through all the evolutionary stages of forming an oxygen-rich atmosphere and complex surface life.

A world orbiting in the HZ of a red giant would find their star to be massive in the sky, but fairly dim nonetheless. The spectrum would resemble an M-type red dwarf, and because these are necessarily old systems it’s more likely that planets will be tidal-locked to the star. So in many respects these are similar to red dwarf systems, though the planets will have longer orbital periods.

For stars of this group, below 0.8 solar masses, the hydrogen in the shell around the core is eventually exhausted and the outer layers collapse back inward, forming a white dwarf.

0.8-8 Solar Masses; G to Late B

Image of the sun in UV. NASA/SDO (AIA)

And now we come to familiar ground, the yellow dwarfs—though many will appear white, but “white dwarf” is already taken. This is pretty broad group, with MS lifetimes from a mere 10 million years to 20 billion. Altogether they account for about 11.9% of nearby stars, and again it’s a skewed distribution with 9/10 being G and F-type stars below 1.4 solar masses.

As I already discussed, only G and late F-type stars could keep a planet in the habitable zone long enough to plausibly form complex life, assuming it takes about as long as it did on Earth. Early F and A-type stars might host at least simple life, but the most massive B-type stars don't even last long enough to allow earthlike planets to completely form and settle down into a stable climate.

ESO/M. Kornmesser

Horizontal Branch and Asymptotic Giant Branch Stars

These stars will form red giants like the last group, and the lightest of these stars could plausibly support life during this stage. But unlike the last group, the core of one of these stars will eventually become dense enough to fuse helium into carbon and oxygen. The expansion of the outer layers ceases and reverses, and the star becomes a hotter, smaller, and dimmer horizontal branch star (the name derives from the distribution of stars on the H-R diagram).

Falk Herwig

After a couple hundred million years at most, the helium in the core is exhausted and the star moves into the asymptotic giant branch (AGB) stage, with fusion once again restricted to shells around the core—now an inner helium-burning shell and outer hydrogen-burning shell. The outer layers reverse course again and continue to expand, brighten, and cool to a greater extent than during the red giant phase.

The helium shell rapidly consumes its fuel and ceases fusing, but helium produced in the hydrogen shell causes it to reignite every 10,000 to 100,000 years. Each time, luminosity spikes and some of the star’s outer layers are completely blown off into space (not explosively, more like very intense solar wind), which can strip away significant portions of the atmosphere of earthlike planets as far away as the Kuiper belt³¹. This makes AGB systems effectively uninhabitable; any earthlike planet that was close enough to be within the "habitable zone" between pulses of helium burning would just lose its atmosphere during the pulses. Perhaps a planet on a wide orbit with a thick atmosphere and high geothermal heat could support simple life, but at that point the star isn't really contributing to the planet's habitability.

ESA/JAXA

After a few million years the star has lost over half its mass and what remains is too deficient in hydrogen for fusion to continue, so the core collapses inwards as some of the remaining outer layers continue to be lost to space. What remains forms a white dwarf, though with a different composition from those formed by less massive stars (not that it shifts the equation much in terms of habitability).

8-30 Solar Masses; Early B to Late O

Technically we could call these “blue dwarfs” but again the name is taken so, whatever, they’re big stars. They have short MS lifetimes of only 500,000 to 10 million years and account for most of the last 0.1% of nearby stars, but are so bright that they’re prominent in the night sky. There’s no main sequence habitability to speak of—the most massive don’t even last long enough to form planets at all—so we’ll jump straight past that to their final days.

Neutron Stars

A star this massive begins fusing helium in its core almost as soon as hydrogen fusion ceases, which prevents core collapse and the associated brightening, though the outer layers still expand and cool. It may eventually blow off those outer layers of hydrogen, leaving the bare core as a Wolf-Rayet star (W-type) with an effective temperature as high as 100,000 K.

Image of WR 124. ESA/Hubble & NASA Acknowledgement: Judy Schmidt (geckzilla.com)

Meanwhile, it will continue to fuse heavier elements in its core past carbon and oxygen to neon, sodium, and magnesium for stars of 8-10 masses, and onwards in heavier stars to silicon, sulfur, argon, calcium, and finally iron (or rather, unstable nickel that soon decays to iron). Smaller stars cannot fuse past magnesium, and for larger stars fusing iron (or nickel) consumes more energy than it produces. In either case, the core no longer produces outward pressure by fusion, and is held up only by electron degeneracy pressure, as with a white dwarf. But fusion continues in shells, feeding more material into the core.

Distribution of elements in an evolved massive star (not to scale). Rursus, Wikimedia

Once the core reaches 1.4 solar masses, electron degeneracy pressure is finally overcome and protons and electrons are forced to merge together into neutrons. The core collapses inwards at astounding speed until it is halted by neutron degeneracy pressure. The combined shockwave produced by the sudden halt and energy produced by nuclear reactions and compression in the core produces a massive explosion, termed a supernova, which blows away the outer layers of the star and either destroys orbiting planets or at least strips away their atmospheres and outer layers; in some cases a close-orbiting companion star or large planet may survive the explosion but be flung away at a few percent the speed of light.

ESO/M. Kornmesser

What remains of the star's core is now an extraordinarily dense neutron star, containing as much as twice the sun’s mass in an object less than 30 km in diameter. It’s largely composed of compacted neutrons—a material sometimes called neutronium—acting in effect as a single immense atomic nucleus, but distinct atoms can exist in the outer layers in highly compressed, degenerate forms ("degenerate" here meaning "not reflecting the usual behavior of matter").

In terms of habitability, neutron stars combine many of the worst aspects of other stars. They necessarily form from a supernova, so no habitable worlds could remain from their previous lives as main sequence stars; they’d have to reform atmospheres, if they survived at all, or new planets would have to form or be captured from elsewhere. And though neutron stars are more massive than white dwarves, the nature of neutronium gives them a much lower heat capacity, so lacking an additional energy source they’ll cool too rapidly to support a long-term habitable zone.

But many neutron stars do have an extra energy source in the form of angular momentum. This momentum is conserved as an immense giant star collapses into a city-sized neutron star, so they are born rapidly spinning, typically completing a revolution every 0.01-10 seconds. Over time, interactions with the star’s magnetic field will cause this energy to be lost as radiation, slowing the spin rate and creating intense beams of light from the magnetic poles all across the electromagnetic spectrum. The magnetic poles do not necessarily align with the axis of spin, so these beams can sweep across the sky. From a distance, these stars appear to emit regular radio pulses, hence the name pulsars.

Most neutron stars form with too little angular momentum to keep producing light this way for more than a billion years, but neutron stars that form in binary systems can gain more energy by accreting gasses from their partner, reaching angular speeds as high as 1 revolution per millisecond, and thus remain productive for much longer.

NASA

Whether or not a planet encounters these beams depends on the particular geometry of its orbit and the star’s spin and magnetic poles. If it doesn’t encounter them, to get enough light to stay warm it would have to orbit extremely close to the neutron star and so experience intense tidal forces. If it does encounter the beams, it will be blasted by gamma rays, X-rays, UV light, and energetic charged particles that could strip away the atmosphere and sterilize the surface.

Even here, though, there may be a chance for life: Some researchers believe³² that if a large rocky planet had a particularly thick atmosphere—as much as 30% of the total mass, for a planet several times as massive as Earth—then a sufficient portion of that atmosphere to protect the surface may be able to survive for billions of years.

The atmosphere would block not only harmful radiation, but visible light as well; so though the surface would be warm enough for liquid water, any life would have to rely on geothermal or chemical energy sources. It would be much like life on the deep sea of Earth, but without the benefit of food dropping from a more productive ecosystem above. Vast, lifeless deserts would separate pockets of simple life living around volcanic hotspots. The chances for complex or intelligent life under these circumstances would seem remote, much less a civilization that could produce spacecraft to breach the thick atmosphere and then withstand the harsh conditions outside.

NASA/JPL-Caltech/R. Hurt (SSC)

It’s possible there is a category of star denser than a neutron star, a quark star, where the internal pressure is great enough to push past neutron degeneracy pressure and decompose neutrons into their constituent quarks, but still not great enough to completely collapse the star to a black hole. There may even be³³ another, still denser category of star, an electroweak star, where the conversion of quarks to leptons in the deepest core provides enough energy to hold back further collapse for upwards of 10 million years. Some stars may begin as rapidly-rotating neutron stars after they supernova, and then convert to quark stars after they’ve lost much of their angular momentum (because the decreased centrifugal force allows their interior to compress more), producing an enormous amount of energy in the form of a quark-nova, which is one possible source³⁴ of gamma ray bursts (loss of angular momentum may also cause a neutron star or similar to collapse into a black hole, though this has yet to be observed).

However, there have been no confirmed observations of such stars (though there are some candidates) and we know so little about the bizarre materials they’re made of that we can’t say much about their likely properties, other than that they’re probably broadly similar to neutron stars from the outside.

>30 Solar Masses; Early O

Finally, we come to the very end of the main sequence, a small category of short-lived, massive stars. Though common in the early universe, they’re now vanishingly rare, accounting for less than 0.01% of nearby stars. The most massive known star, R136a1, is 315 solar masses, and it seems unlikely that any star could ever get much bigger before the light produced by the core was great enough to blow away the outer layers. Lower metallicity in the past may have raised this limit, and in the very early universe there may have been³⁵ quasistars up to 10,000 solar masses that outwardly appeared to be gigantic stars but were in fact clouds of gas falling into black holes formed in their cores.

Note that despite being the most massive star, R136a1 is fairly small in size (~35 solar radii) compared to the largest red giants (~14 solar masses, ~2150 solar radii) and both are dwarfed by quasistars (~7200 solar radii). Sauropodomorph, Wikimedia

Black Holes

Rare though high-mass stars are, they’re the only ones large enough to produce the objects that will eventually come to dominate the universe: black holes. After one of these stars undergoes a supernova, enough mass remains in the resulting neutron star—about 3 or more solar masses—that its gravity overcomes even neutron degeneracy pressure (and whatever barriers may remain beyond that) and it continues to collapse, perhaps without limit. Within an area around the former star known as the event horizon, the gravity is so intense that the geometry of space only allows for travel towards the center, not away; so no light or anything else can escape.

Exactly what happens inside the event horizon is unclear; general relativity predicts an infinitely small singularity, but some physicists believe that quantum mechanical effects may eventually halt the collapse, or even odder geometries may result from intense time dilation. For now, we can't really say much for sure. We do understand (and have partially confirmed with observation) that the strong gravity can still have odd effects outside the event horizon; objects can orbit along spiraling paths that wouldn't be possible elsewhere, and light is curved around the black hole such that from every direction it appears as a dark orb surrounded by a ring of light.

Modelled appearance of a black hole with an accretion disk. NASA’s Goddard Space Flight Center/Jeremy Schnittman (see there for detailed description of what causes these optical effects)

Especially massive (>40 solar masses) and metal-poor stars experience a collapse so forceful that it cannot be even briefly halted and the star collapses directly to a black hole without a supernova. Even more massive (130-250 solar masses) and metal-poor stars can experience a pair-instability supernova, which occurs when quantum mechanical processes in the core consume some of the star’s light output, which reduces outwards pressure, which causes the core to partially collapse inwards, which rapidly accelerates fusion, and the star can be completely blown apart with no remnant left.

Remnants left lone stars at the end of their lives (mass exchange between close-orbiting binary stars complicates their evolution). "Electron capture collapse" produces a neutron star. Bear in mind that stars to the right of this diagram are increasingly rare, so don't take area as a strong indication of how often these occur. Fulvio 314, Wikimedia, based on Heger et al. 2003

Black holes themselves produce almost no light. Quantum mechanical effects at the event horizon can cause energy loss by Hawking radiation, but the total luminosity is inverse to the black hole’s mass, so that it does not emit enough light to be realistically capable of warming a planet to habitable temperatures until the last minutes of its life (which, for any current stellar-mass black hole, will not occur until long past the point when all stars and planets are long gone).

However, when matter falls into a black hole it is stretched into an accretion disk, where tidal forces and friction can heat it enough to emit light, and in rare cases even undergo fusion³⁶. A stellar-mass black hole can form an accretion disk by consuming the mass of a binary partner, but such a disk would emit high amounts of XUV radiation, have an inconsistent total light output, and last for only 10s of millions of years.

ESO/L. Calçada/M.Kornmesser

But many galaxies host a supermassive black hole (SMBH) at their center, formed in the early universe from the combination of many black holes and stars to form an object a million solar masses or larger. These can sustain a larger but cooler disk for 100s of millions to billions of years (a moderate form of the active galactic nuclei we discussed last time), and in the outer regions of the disk some of the dust could plausibly form planets³⁷ (sometimes called "blanets"). An SMBH like Sagitarrius A* could have thousands of these planets orbiting around 1 to 20 light-years from its center, with orbital periods of millions of years; even planets in very similar orbits will encounter each other very infrequently, and so they won't clear their orbits in the same way as planets in star systems do, and will form more of a swarm of intersecting orbits rather than a neat sequence.

The "habitable zone" of this system (somewhere around a light-year out, perhaps; there's no strict mass-luminosity relation to follow here) will still receive high XUV radiation. But perhaps, as with pulsars, a planet could form with a thick atmosphere that takes the brunt of the radiation while enough heat reaches the surface to sustain habitable temperatures.

Even if a planet isn't heated primarily by light from the accretion disk—if it, say, orbits a star that is itself in a distant orbit of the SMBH—that light may still be enough³⁸ to aid in photosynthesis or abiogenesis as much as a thousand light-years out.

Perhaps the biggest issue is that the region around an SMBH tends to be densely populated with stars on chaotic orbits, and the presence of an accretion disk implies at least some objects falling into the center, passing through the planet swarm. There's a significant risk that a planet orbiting the SMBH or a nearby star could be shifted out of the habitable zone by an encounter with a passing star long before complex life could develop. The gravitational influence of the SMBH could also interfere with the orbits³⁹ of planets around nearby stars.

Finally, there is one bizarre proposal⁴⁰ for how life might survive near a more quiescent black hole with no accretion disk. A planet in a very tight orbit around a rotating black hole will see the cosmic microwave background blueshifted (the inverse of redshift) into visible light, both due to gravitational time dilation and the Doppler effect due to its immense orbital velocity. There is even⁴¹ a "habitable zone" where the planet receives light comparable to what Earth receives from the sun. The light would be concentrated on the side of the planet facing the direction of the planet’s travel, while the black hole itself—occupying a quarter of the sky—would pull heat away from the planet, creating a temperature gradient that could drive a dynamic climate.

But there are some glaring issues for such planets: in order to allow for a planet to exist within this habitable zone without being torn apart by tidal forces (I won't even comment on issues caused by tidal heating), the black hole would need to have⁴² a mass of at least 163 million solar masses and a rotation near the theoretical maximum. This will cause intense time dilation, such that one year on the planet corresponds to thousands of years outside the black hole's influence; so any such planet in the universe today would be only a few million years old in its reference frame. Worse, the CMB will dim over time, causing the HZ to migrate inwards such that a planet near the inner edge today will pass the outer edge in roughly 6 billion years—which to the planet's perspective is barely over a million years (decay of the planet's orbit due to gravitational radiation may somewhat extend its habitable period, but by the same token will plunge it past the event horizon within a few million years in its perspective). And, of course, any material entering the black hole over that time—let alone the formation of a full accretion disk—could be catastrophic for the planet, given the extreme velocities the debris will reach under the black hole's gravity.

Prospects may be better for a smaller black hole with a companion star, as the same blueshifting of light could focus the star's light onto an orbiting planet (though it may also shift much of it into XUV radiation). But overall, even though black holes may ultimately harbor most life over the universe's lifetime, that life will probably have to emerge elsewhere first.

0.013-0.08 Solar Masses; Y to Very Late M

Concept of CFBDSIR 1458+10. ESO/L. Calçada

To finish off our tour of stars, let’s leave supermassive stars and their remnants behind and return to the least massive members of the star family, brown dwarfs. At this point it’s more convenient to state their mass in relation to Jupiter, which is 1/1,047 times as massive as the sun; so these bodies are around 13 to 80 Jupiter masses (the upper boundary is a bit fuzzy and may be anywhere from 70 to 96 Jupiter masses depending on the star's metallicity, so people usually just state it as a round number in whatever unit they're using). It’s hard to say exactly how common they are because they’re so dim, but they may be comparable in number to all main sequence stars put together.

Brown dwarfs are sometimes called “failed stars” because the pressure in their cores is too low to fuse ordinary lone-proton hydrogen into helium. However, they can fuse deuterium and—for brown dwarfs over 65 Jupiter masses—lithium. This is sufficient to initially warm the dwarf to the temperature and luminosity of a late M-type star, but the abundances of deuterium and lithium are so low (about 20 parts per million and 1 part per billion, respectively, in undisturbed gas in our galaxy) that fusion tapers off⁴³ after a few 100 million years at most—only 10s of millions of years in the smallest dwarfs.

Concept of 2MASS J22282889–4310262. NASA/JPL-Caltech

They gradually cool off thereafter, exiting the M spectral type for the recently-named L-type. After 100 million to 10 billion years they enter the T-type when they cool past around 1300 K, low enough for methane gas to form in their atmosphere. After their initial red, this blue methane turns most dwarfs magenta, with some variation by composition; few brown dwarfs are actually brown. Though the surface is still hot enough for phenomena like iron rain⁴⁴, these dwarfs emit very little visible light. Finally, dwarves below around 500 K are considered Y-type, a category that also includes objects below 13 Jupiter masses—conceivably as small as 1 Jupiter mass—that form from collapsing gas clouds like stars but are too small to ever experience any type of fusion.

NASA/JPL-Caltech

In terms of habitability, brown dwarfs suffer from many of the same pitfalls as white dwarfs. The habitable zone sweeps inwards over a period of a few billion years, and from the start is close enough to the dwarf for tidal heating to be an issue for even moderately eccentric planets. Within a billion years²⁹ the eccentricity constraints are even more stringent than for a white dwarf and the habitable zone is approaching the Roche limit for an Earth-sized planet; the orbital radius at which tidal forces will overcome the planet’s gravity and tear it apart into a ring of debris. Even during the best period for habitability, the peak light output from the dwarf is far into the infrared, making photosynthesis difficult if not impossible.

Brown dwarfs may be of some interest to interstellar civilizations simply because they’re so common and could provide convenient sources of resources, but they’re unlikely to host any complex life of their own.

However, note that all of this only applies to brown dwarfs as they exist today. In the far future, when average metallicity of new stars is several times higher than today, newly formed brown dwarfs may be able sustain protonic fusion⁴⁵, making them proper main sequence stars with extremely long lifetimes (incidentally this also means⁴⁶ there are some old, high-mass brown dwarfs around today that were too metal-poor when they formed to enter the main sequence, up to a theoretical maximum⁴⁷ of 0.092 solar masses with zero metallicity). But these stars would also have very low effective temperatures, as low as 273 K for a star of 0.04 solar masses. So in terms of habitability they’re mostly no better than current brown dwarfs, but there may still be a range of masses too low to form MS stars now, but high enough that when they do, they’ll produce just enough light to possibly support life.

Multiple-Star Systems

Concept of HD 98800. NASA/JPL-Caltech/T. Pyle (SSC)

That about wraps up our tour of star varieties, but stars don’t always appear alone. Many stars form in pairs, or in groups observed to be as large as 7. We used to believe that the majority of all types of stars are found in multiple-star systems, but current research shows that the exact frequency depends greatly on mass. Among nearby stars⁴⁸ within the galactic disk, over 80% of systems with an O-type primary star have companion stars, while the same is true for only 44% of sunlike star systems and less than 25% of red dwarf or brown dwarf systems (note that this is a count of systems, not stars, which means that the total proportion of individual red dwarfs that are in multiple-star systems is higher). Higher-mass multiple star systems are also more likely to include more companion stars within each system.

Age also plays a role, as stars that form with companions may lose them over time due to gravitational interactions with other stars. Old Population II stars off the galactic disk seem to particularly lack companion stars, but whether because they’ve had more time to lose their companions or their lower metallicity caused them to form with fewer companions in the first place is not yet clear.

Barring any brief upsets, the 2 stars in a binary system both settle into stable elliptical orbits around their common barycenter—center of mass for the system—with equal eccentricities and orbital periods, such that a straight line between the two stars always passes through the barycenter. If they’re of unequal mass, the more massive star orbits closer to the barycenter; for very unequal masses the barycenter may be inside the more massive star.

Zhatt Wikimedia

There are no particular constraints on the distance separating the two stars; they can be light-years apart or so close that they share a common atmosphere. But in the former case it will be much easier for another passing star to pull the binary apart, and in the latter case angular momentum will be lost to friction over time and the two stars will collide and merge. Current observational data indicates that sunlike stars tend to be separated by 10s to 100s of AU, with orbital periods of decades to centuries, while red dwarfs are more likely to be an order of magnitude lower on both counts.

Star systems with more than two stars are arranged hierarchically: A trinary system will have one binary pair, and then the barycenter of that pair will be in a binary relationship with another, more distant star. For a 4-star system you can replace that third star with the barycenter of a binary pair, or have the common barycenter of the whole trinary in a pair with another star. And then you could replace that star with a binary, or have two trinaries paired, and so on. A good analogy for these hierarchies is a child’s mobile; each rod is balanced on the center of mass of everything hanging from it, just as the barycenter of every pair in a multiple star system is the center of mass for everything involved in the pair.

Diagram of the Castor system (NASA/JPL) with a chart of its hierarchy (Wikipedia). Castor A, B, and C are all binary systems, the barycenters of A and B orbit each other, and then that common AB barycenter and the C barycenter orbit each other.

Newborn stars may briefly exist in chaotic non-hierarchical associations, but before long these will either settle into a hierarchy or eject extra stars out of the system until they do. Some theoretically stable configurations of non-hierarchical trinary systems have been mathematically described, but none have been observed in reality and they require such specific starting conditions that I wouldn’t hold my breath.

So, can life exist in these multiple-star systems? Planets can form in binary systems in two main types of orbits: S-type, where they orbit closely to one star with a much smaller orbital radius than its distant companion star; and P-type or “circumbinary”, where they orbit distantly around the system barycenter with a much wider radius than either of the stars.

Philip D. Hall, Wikimedia

S-Type

For a widely separated binary, S-type planets can form just as frequently as planets around a lone star, and with the same properties. If the companion star is dim, the inhabitants of such planets may not even realize they are in a binary system until they develop astronomy and sufficiently powerful telescopes. But if the companion star orbits closer, its gravitational influence could interfere with the formation of planets or knock them out of their orbits after they form.

Concept of Proxima b. ESO/M. Kornmesser

Modelling of binary systems⁴⁹ indicates that Earthlike S-type planets should still be possible with companion stars as close as 5 AU, but while planets have been observed⁵⁰ in such systems, there is a generally a paucity of S-type planets for systems with separations less than 100 AU, and debris disks—which imply the presence of solid bodies like planets—are similarly less common⁵¹ below 50 AU of separation.

But these numbers are based mostly on observations of sunlike stars. More generally, theoretical modelling of these systems indicates that the extreme limit of long-term stability for the semimajor axis (average orbital radius, roughly) of an S-type orbit is about 1/4 the semimajor axis of the binary pair for equal-mass stars. If one of the stars is more massive than the other, the stability zone increases for planets orbiting the more massive star and decreases for planets orbiting the other star. Eccentricity of the binary orbit will shrink the stability zones for both stars. I'll discuss how to calculate the limits of stability for both S-type and P-type planets more precisely later in this post.

But even if a planet's orbit is "stable" in the sense that it won't be ejected from the system, that doesn't mean it's locked in place. Earth experiences subtle shifts over thousands of years in its axial tilt, orbital eccentricity, and the relative timing of its solstices and closest approach to the sun, collectively called Milankovitch cycles, due to the gravitational influence of the other planets (mostly Jupiter). These cycles can plunge the planet into and out of ice ages and shift the positions of deserts and rainforests. In a binary system, the influence of a nearby companion star could cause similar cycles⁵² that may be both more rapid and greater in amplitude, shifting between warming and cooling the planet by several °C every few thousand years. In some cases the planet may even alternate between forming ice caps at the poles and forming an "ice belt" near the equator.

Modelled surface temperature (top) and ice accumulation (bottom) over 500,000 years for an earthlike planet orbiting Alpha Centauri B with on an orbit initially inclined by 30° relative to the binary orbit. Quarles et al. 2021

Even if life on the planet can adapt to these shifts in climate in regular circumstances, they may make the planet more prone to "snowballing"; freezing over completely, a state that can be difficult to recover from. But this needn't be a case for all S-type planets. In general it seems these extreme climate cycles are more common where:

The binary has a small semimajor axis (below ~50 AU for sunlike stars).
The binary has high orbital eccentricity (above ~0.2).
The orbit of the planet around its star is highly inclined relative to the binary orbit between the stars (above ~5°).
The planet orbits the less massive of the two stars.

In most cases⁵³ the companion star does not contribute enough light to affect the habitability of an S-type planet. However, were there a planet orbiting a red dwarf with 0.1 solar masses at 0.1 AU (outside the typical habitable zone) and the dwarf was itself orbiting a sunlike star at 1 AU, the planet would receive about 11 times as much light from the larger star, putting it back in the HZ. In such a case it might even be better to treat the planet like a moon of a gas giant in terms of habitability, though the presence of constant dim light on one side of the planet even at “night” (as it will likely still be tidal-locked to the smaller star) and variance in distance from the primary star of 0.1 AU could both lead to interesting climatological effects.

This calculator can give you good estimates for HZs and stable regions for S-type (and P-type) orbits, but note that we’ll discuss the wrinkles of habitable zones in more depth in the next post. Roughly half of all binary systems⁴⁹ should be widely separated enough to support habitable Earthlike planets in stable S-type orbits (and 10% should be close enough for such worlds in stable P-type orbits).

P-Type

IAU/L. Calçada

Once the stars are within a few AU of each other, they can start to form circumbinary planetary systems similar to those for lone stars, and sunlike stars separated by less than about 0.2 AU should be able to form P-type planets in the habitable zone. Several planets have been observed⁵⁴ in P-type orbits. Curiously enough, these planets seem more likely⁵⁵ to form near the inner limit of a stable orbit—though this may be in some part due to biases in current detection methods—and are less likely to form around binaries with very small separations and orbital periods less than 10 days—perhaps due to tidal effects inhibiting the formation of planets or ejecting any planets that do form. When planets do form⁵⁶ around very close-orbiting binaries, it's likely that they will be more massive and fewer in number on average compared to single-star systems.

NASA/JPL-Caltech/Univ. of Ariz.

As before, these values can vary with different stars and configurations, with the inner limit of a stable planetary semimajor axis being around 2.3 times the binary semimajor axis for equal-mass, low eccentricity stars. But in this case, the difference in masses has little effect and the eccentricity is much more important.

Intriguingly, retrograde orbits may actually be more stable⁵⁷, though for large planets so close to the system barycenter they’ll also be exceedingly rare. A captured planet could end up in such an orbit, but then its history as a rogue planet could negatively affect its habitability in the present.

Generally speaking, for all purposes of habitability the star pair in such a system can be treated as a single star with a luminosity equal to the sum of the luminosities of the two stars. There will be some climate variation on a P-type planet’s surface over the period of the pair’s orbital period, but not enough to significantly impact habitability⁵⁸. If the planet’s orbit is in the same plane as that of the binary, one of the stars may eclipse the other, but the change in surface light would be comparable to seasonal changes on Earth, and much briefer.

If the two stars are of different masses, then they will evolve in different ways, which may or may not be beneficial for the long-term habitability of the planet depending on the particular configuration. And if one of the stars in a close-orbiting binary becomes a white dwarf, there is a chance it could accrete gas from its companion, resulting in a nova—wherein enough gas accumulates to undergo fusion in a shell above the degenerate white dwarf core, producing a period of intense light and bombarding the system with radiation and highly accelerated gas—or a type Ia supernova—wherein the white dwarf surpasses 1.4 solar masses and collapses into a neutron star, triggering rapid fusion in the surrounding mass and thus outputting enough energy to destroy the system entirely and eject the companion star.

T-Type

As a third option, some authors have proposed Trojan planets, in the L4 or L5 Lagrange point of one of a binary pair—that is, occupying the same orbit as one of the paired stars but offset by 60 degrees ahead or behind, where the gravitational influence of the stars will tend to keep it stably positioned. We might call this a “T-type” orbit.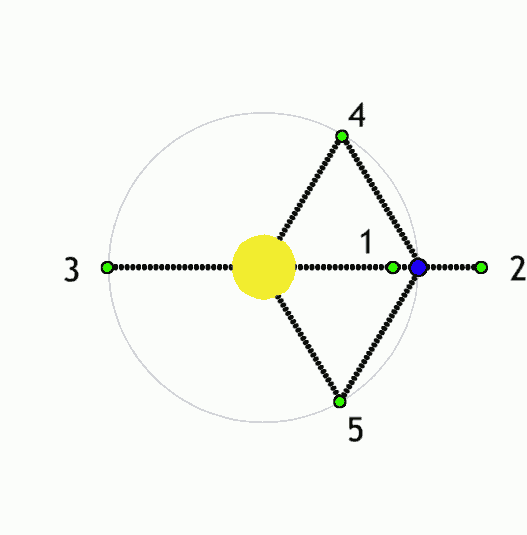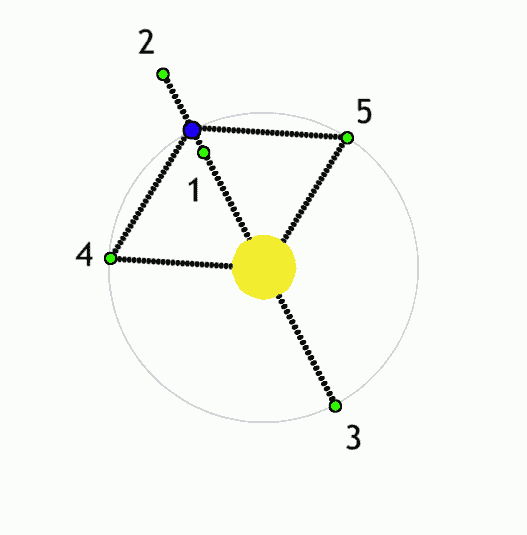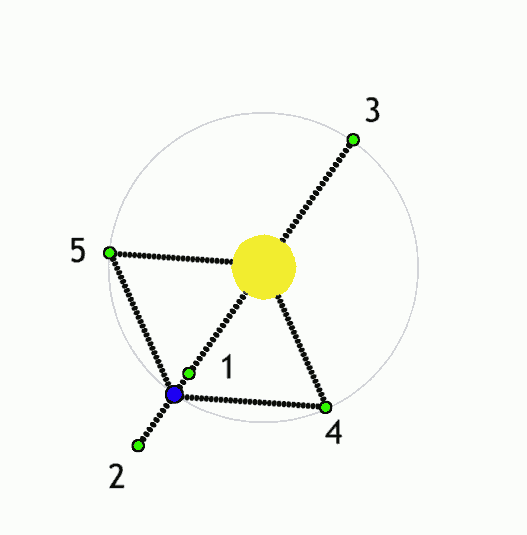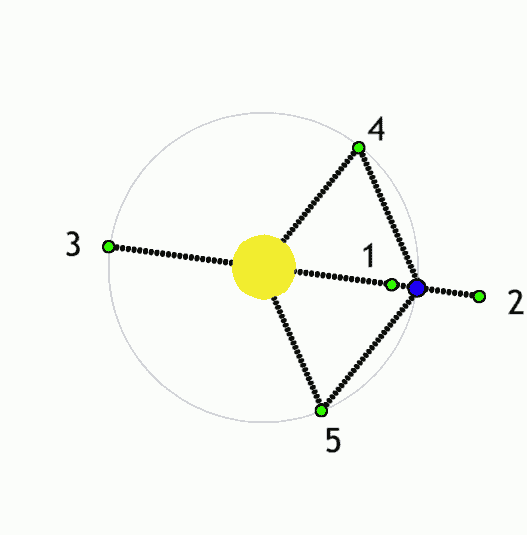

Motion of the Lagrange points for a large body (yellow) with a smaller companion (blue); points 4 and 5 are stable. Anynobody, Wikimedia

However, for such an orbit to be stable in the long term⁵⁹, the mass ratio between the two stars would have to be greater than 25. If the smaller star is a minimum-mass M8 star—with 0.08 solar masses—then the larger star cannot be smaller than 2 solar masses, making it a late A-type with a lifetime of about 1.5 billion years, possibly too short for complex life to develop.

If you do decide to include such a system in a story—say, if it is visited by an interstellar traveler—then note that, because the stars and planet will necessarily all be equidistant from each other, the larger star will be about 47,000 times brighter than the smaller one, or 4.7 million times brighter if only visible light is counted. If the planet were receiving the same amount of light from the primary star as the Earth did from the sun, the secondary would be only 1/12 as bright as the moon in Earth’s night sky.

However, if the secondary in this system is a brown dwarf or gas giant below 0.05 solar masses, then the primary star can be small enough to give planets a longer window to develop complex life. The system should be stable⁶⁰ so long as the inclination is below ~60° relative to the primary’s equator and eccentricity is fairly low. Indeed, some models indicate⁶¹ such planets should be common, though so far none have been observed.

Trinary

Concept of surface of Gliese 667Cd. ESO/M. Kornmesser

Finally, it is possible for planets to appear in systems of 3 or more stars, and a handful of such planets have been observed. Typically these planets will only orbit one or a pair of stars in such systems in the S- and P-type orbits we’ve discussed, with the distant third star or companion binary having little impact. But it may be possible for a habitable planet to orbit around three stars, if quite rare.

Theoretical modelling⁶² indicates that, for three stars of equal mass, the orbital period of the distant third star with the binary pair must be 4.37 times greater than the orbital period of the binary. This ratio of orbital periods can be as low as 2.37 for greater mass ratios, though that case would require the largest star to be 98 times the smallest.

If we use 3 equal-mass sun-sized stars, and put 2 of them in a binary with a period of 1 day (0.016 AU semimajor axis, probably near the limit before they join atmospheres and merge) with the third orbiting on a comfortable 5-day orbit (0.039 AU semimajor axis between this star and the barycenter of the binary) then a planet would receive insolation similar to Earth at a distance of 1.73 AU, over 10 times the semimajor axis of the trinary system—probably a safe distance.

What the stability constraints are for systems with 4 or more stars is something I haven’t seen any theoretical work on, so I can’t speak to the potential habitability of planets in such a system—though you can generally assume that distant companions won't have much impact on the habitability of compact single, binary, or trinary star systems.

Calculating Stellar Properties

As we've seen, there are many patterns to how stars form and evolve, but also many subtle variations to these patterns. Constructing a full model of how stars evolve is a daunting task even for researchers, so for our purposes we'll have to rely on approximations. Many of these have been developed over the years, and in general there's a sliding scale of greater complexity to get greater accuracy and precision, so I'll pick out a few different options to choose from.

A few notes:

I'll only be discussing main sequence stars here. Evolution of stars beyond the main sequence becomes very complex, with huge changes in luminosity and size, loss of mass by the star, and abrupt shifts between stages as the nature of fusion in the core changes, and so is essentially impossible to simply approximate.
For simplicity, I'll be using units of solar luminosity and solar radii in addition to solar masses; in each case this describes the value of that property relative to the sun.
I'll leave habitable zone calculations for a later post.
If some of these look pretty daunting to implement on your own, don't worry; I'll be adding every formula that appears in this series to my worldbuilding spreadsheet. I show the raw math here simply as a resource for those who do wish to try and construct these sorts of models on their own.

Simple Approximations

Main sequence stars conveniently have a pretty close relationship between mass, luminosity, and effective temperature, so we can roughly predict the latter two values for a main sequence star based on mass.

For effective temperature, this simple mass-temperature relation works fairly well for stars between 0.2 and 20 solar masses:

T_eff = effective temperature (K)

M = star mass (solar masses)

The mass-luminosity relation is a bit more complicated, so it's best to use a few different formulas for different mass ranges:

L = luminosity (solar luminosity)

M = star mass (solar masses)

Luminosity, effective temperature, and a star's radius are all linked by the Stefan-Boltzmann law (the light emitted from each point is determined by temperature, so the total luminosity is determined by temperature and surface area, and surface area is determined by radius). So we can determine radius from luminosity and temperature (or temperature from luminosity and radius, as will be necessary in the next section):

R = star radius (solar radii)

L = luminosity (solar luminosity)

T_eff = effective temperature (K)

(The full form of the Stefan-Boltzmann law includes some additional constants, but using units scaled to the sun—a system already governed by this relation—lets us avoid those)

The total fuel a star has available (and the portion of that fuel that is burned in its lifetime) is determined by its mass, and the rate it burns through that fuel determines its luminosity, so we can also ballpark the time it will spend in the main sequence based on these properties:

t_MS= main sequence lifetime (billions of years)

M = star mass (solar masses)

L = luminosity (solar luminosity)

Complex Approximations

Simple approximations work alright in a pinch, but can be fairly inaccurate in some cases, and in particular don't work well for stars much smaller or larger than the sun. Luckily for us, astronomers have long been looking for ways to predict the properties of stars with higher accuracy, without always having to construct complex models.

First off, these formulae⁶³ are a bit more accurate for main-sequence stars between 0.179 and 31 solar masses:

L = luminosity (solar luminosity)

M = star mass (solar masses)

For stars of 1.5 solar masses or less, we can then find the radius:

R = star radius (solar radii)

M = star mass (solar masses)

For stars over 1.5 solar masses, we instead find the effective temperature:

T_eff = effective temperature (K)

M = star mass (solar masses)

In either case, we can then use the Stefan-Boltzmann law to find the remaining parameter.

Evolutionary Models

Of course, stars change as they age, even within the main sequence, so any model that doesn't for the star's age can only get so accurate. The full evolution of all different types of stars is very complex to model, but we can approximate a few specific cases.

First off, for many stars the main sequence can be approximated as a linear evolution, proceeding at a steady rate from the zero-age main sequence (ZAMS) parameters at the start of the main sequence to the terminal-age main sequence (TAMS) parameters. These formula⁶⁴ should work reasonably well for stars between 0.74 and 10 solar masses:

First, we can better estimate the timeframe of the main sequence. First, the age when the main sequence begins:

t_ZAMS = age at start of main sequence (billion years)

M = star mass (solar masses)

Then, the age when it ends:

t_TAMS = age at end of main sequence (billion years)

M = star mass (solar masses)

Luminosity at the end of the main sequence can be approximated like so, again in slightly different forms for different mass ranges, and luminosity at the start of the main sequence is roughly half that value.

L_ZAMS = luminosity at start of main sequence (solar luminosity)

L_TAMS = luminosity at end of main sequence (solar luminosity)

M = star mass (solar masses)

The formulae for temperature are a tad more complex:

T_eff,ZAMS = effective temperature at start of main sequence (K)

T_eff,TAMS = effective temperature at end of main sequence (K)

M = star mass (solar masses)

We can then linearly interpolate both luminosity and effective temperature for any age in the main sequence like so:

X = parameter (luminosity or temperature) at current time (any unit so long as X_ZAMS and X_TAMS use the same)

X_ZAMS = (luminosity or temperature) at start of main sequence

X_TAMS = (luminosity or temperature) at end of main sequence

t = current age of star (any unit so long as t_ZAMS and t_TAMS use the same)

t_ZAMS = age of star at start of main sequence

t_TAMS = age of star at end of main sequence

And finally, we can determine the star's radius with the Stefan-Boltzmann law.

For lower-mass stars we can get a bit more precise; this rather ugly set of formulae⁶⁵ will approximate the first 12.6 billion years of luminosity evolution on the main sequence (or up to the end of their lives, at the top of the mass range) for stars of 0.08 to 1 solar masses:

L = luminosity (solar luminosity)

t = star age (billion years)

M = star mass (solar masses)

For stars that last longer than 12.6 billion years, we can approximate the luminosity at the end of the main sequence like so⁶⁶:

L_TAMS = luminosity at end of main sequence (solar luminosity)

M = star mass (solar masses)

The star's lifetime can be approximated like so:

t_MS = main sequence lifetime (billion years)

M = star mass (solar masses)

And then we can use linear interpolation like before to find values in between, but in this case using the output of the above formula at 12.6 billion years in place of the ZAMS values.

For effective temperature and radius, we'll have to linearly interpolate for the whole main sequence, using either the effective temperature formulae above for stars over 0.74 solar masses, or these radii formulae:

R_ZAMS = luminosity at start of main sequence (solar luminosity)

R_TAMS = luminosity at end of main sequence (solar luminosity)

M = star mass (solar masses)

And then interpolate (for simplicity, ignore any pre-main sequence evolution and set t_ZAMS = 0) and determine the other value with the Stefan-Boltzmann law.

That's about as much as is reasonable to communicate in a blog post (if not a little beyond it). As a final option, I've now implemented the extensive formulas of this paper⁶⁷ as a standalone tool; see the supplement.

Empirical Data

Ultimately the most accurate way to estimate a fictional star's properties is to just copy a real star. Wikipedia has fairly extensive lists of stars that are, for the most, part, reasonably accurate.

You can also consult the tables here⁶⁸, showing average properties for each spectral subtype across the main sequence, and even into the brown dwarfs (the word wrapping can make it hard to read in browser, I suggest copying it out to a text file or spreadsheet). Most of the values listed there are various measures of the stars' colors and spectra, but the most important for us are "SpT", the spectral type; "Teff", the effective temperature in Kelvin, "logL", the logarithm of the luminosity in solar luminosities (recall that if log(x) = y, then 10^y = x); "R_Rsun", the radius in solar radii; and "Msun", the mass in solar masses (you may also want to note "BCv", the bolometric correction factor, which may be useful when determining the visual appearance of the star down the line)

Or, if you want a more instantly readable table, there's a pretty decent—if less detailed—one on the Atomic Rockets website.

There are a couple downsides to this approach: For one, there are no stars more than 13.8 billion years old, so some types of stars simply don't exist yet, and we have no reference for them other than computer models. Our sample of low-mass stars represents only the earliest stages of their evolution, and we can expect that the average luminosity of M-type stars will be significantly higher in 100 billion or 1 trillion years' time.

There are also some errors and inconsistencies in our measurements, so it's probably best to find more well-known and nearby stars, or use the averages.

To wrap this up, here's a comparison between what properties these different methods predict for a broad range of main-sequence stars:

Binary System Orbits

Though I spoke in generalities about the limits for stable orbits in binary systems, we can estimate these a bit more precisely:

First off, the period of the orbit between the two stars—or any two bodies, really—can be determined by Kepler's 3rd Law, which relates the semimajor axis of the orbit (for a circular orbit, this is just the distance between the stars) to its period (and, via Newton's law of gravitation, to the combined mass of the stars). Take note of this one, it'll pop up a lot in the next few posts:

P = orbital period (years)

a = semimajor axis (AU; average distance between Sun and Earth)

M, m = mass of the two stars (solar masses)

(As with the Stephan-Boltzmann law, we can avoid dealing with any bothersome constants by using units scaled to an existing orbit, that of the Earth around the Sun.)

If the orbit has some eccentricity, the distance between the stars can vary; I'll explain the math behind orbits a bit more in the next post, but in short you can still regard the semimajor axis as a sort of 'average' separation, and the greatest deviation in the distance between the bodies from the semimajor axis will be equal to [semimajor axis] * [eccentricity] (e.g., if 2 bodies have an orbit with a semimajor axis of 2 AU and an eccentricity of 0.3, the distance between them will vary from 1.4 AU to 2.6 AU).

Both stars in a binary system (and, again, any orbit really) orbit a common barycenter. To reiterate, they do not independently orbit the barycenter as is commonly misunderstood; they both have the same orbital period and eccentricity, the barycenter is always directly between them, and the ratio of their distances from the barycenter is always equal to the ratio of their masses (e.g. if one of the stars is half the mass of the other, it will be twice as far from the barycenter). Really the barycenter is just a convenient reference point to describe the average momentum of the whole system and the orbit of P-type planets. If we don't have any P-type planets to worry about and we don't much care about how the system appears from afar, we can mathematically describe the system such that one of the stars is stationary and the other follows an elliptical orbit, and Kepler's laws still apply; this may be more convenient for describing how observers on an S-type planet see the companion star.

Anyway, we can estimate the limits of long-term stability for planetary orbits in binary systems based on the semimajor axis and eccentricity of the orbit between the stars and the ratio of the star's individual masses to that of their combined mass (see also tables 3 and 7 here⁶⁹; there have been many attempts to model this for various configurations, some producing smaller limits, but this seems to be a typical result).

This is the maximum semimajor axis for an S-type planet (note here that the "companion star" is the star the planet is not orbiting):

a_max = maximum stable semimajor axis for an S-type planet (any unit so long as a_bin is the same)

a_bin = semimajor axis of the binary

m = (mass of the companion star) / (total mass of the binary)

e = eccentricity of the binary

And this is the minimum semimajor axis for a P-type planet:

a_min = minimum stable semimajor axis for a P-type planet

a_bin = semimajor axis of the binary

m = (mass of the less massive star) / (total mass of the binary)

e = eccentricity of the binary

Back Home

Taking it all in, it seems we can order all the candidates for stars that might support life as ideal (G- and K-type main sequence stars), challenged (F- and M-type stars, red giants, blue dwarfs), marginally plausible or short-lived (A- and B-types, white dwarfs, brown dwarfs, pulsars, supermassive black holes) and borderline impossible (O-types, AGB stars, stellar-mass black holes). For now it seems like only the the first two categories could plausibly develop complex and intelligent life, but that may just reflect our limited perspective; we only know of one type of life, with biochemistry optimized for the environment of a G-type star, and while there are robust theoretical reasons to doubt that life of any sort could survive in some of the harsher environments we've discussed, we can't really be sure without more empirical data. But on the other hand it would make sense that intelligent life—possibly the first intelligent life in this region of the universe—developed under the most hospitable conditions available.

With that in mind, let’s put our example species an ideal system. We don’t know yet what the eventual language of this species will be like, so for the interim let’s just call the system “Teacup”. Given the option, we might as well choose a star that will give us a longer habitable periods and closer-spaced planets that will make interplanetary travel easier, so let’s make Teacup A a K5V orange dwarf modeled after 61 Cygni A. Compared to our sun it has 70% the mass, 66% the radius, and 15% the luminosity.

After an initial warm period of 100 million years, it goes through a couple more variations and then after about a billion years settles into the main stage of its life with an effective temperature of around 4,500 K. A planet comfortably within the habitable zone at this point can expect to spend about 20 billion years there, and potentially twice as much if very well placed. After 44 billion years Teacup A will transition to a red giant, expanding over 3 billion years to a radius of 9 AU and a luminosity 2,500 times that of the sun, then collapse into a helium white dwarf.

Our reference star, 61 Cygni A (lower middle) compared to the sun (left) (upper right is 61 Cygni B, a K7V star). I'm pretty sure it's depicted as too red here, but it's good for size comparison. RJHall, Wikimedia

To spice things up just a little, we’ll give this star a companion, Teacup B, and make it an M3V star modeled after Gliese 581. So that’s 31% the mass, 30% the radius, and 1.3% the luminosity of the sun (44%, 45%, and 8.7% respectively with regards to Teacup A) though most of that luminosity is in the infrared given its effective temperature of ~3,500 K, leaving it with just 0.2% the visible light output of the sun. Teacup B is sufficiently large that by the time any intelligent life arises on Teacup A, it will have quieted down and settled into the main sequence, where it will remain for about 300 billion years.

Gliese 581 (right) compared to the sun (left). RJHall, Wikimedia

I'll give the orbit between the stars a semimajor axis of 150 AU and an eccentricity of 0.15, such that the separation between them will go from 127.5 AU to 172.5 AU each orbit. This puts Teacup B comfortably out of the way of interfering with planet formation around Teacup A—or the reverse happening—but close enough to make a good first step for interstellar travel and maybe give early astronomers something to ponder. Given this semimajor axis, the mass ratio between the stars, and the fairly low eccentricity, we can expect S-type planetary orbits around Teacup A to be stable out to around 42 AU and those around Teacup B to be stable out to 25 AU (P-type orbits are stable beyond 465 AU from the barycenter, but I don't intend to add any such objects for the moment).

Kepler's 3rd Law gives us an orbital period of 1,828 years (Earth years, that is; we’ll establish the year length for our habitable planet in another post). Teacup B will spend more time at the outer part of its relative orbit around Teacup A than at closer approach, but for now we won’t bother calculating the specifics.

Alright, that should about do it for stars. After a quick review of orbital mechanics, we’ll look at the formation of planets and moons, and dig a bit deeper into what the constraints for a habitable planet really are.

In Summary

More massive stars are generally hotter, bluer, brighter, and have shorter lifetimes.
Stars spend the majority of their lives on the main sequence, with a direct relationship between luminosity and effective temperature.
Stars are brighter at both the start and end of their matter-fusing lifetimes, and gradually brighten while on the main sequence.
Habitability for complex life during the main sequence is ideal for K and G-type stars, plausible but challenged for M and F type stars, and unlikely for larger or smaller stars.
Tidal-locked worlds could reasonably be habitable, even around small red dwarfs.
Some red giants and blue dwarfs could be habitable, but all other post-MS stars are unlikely to support complex life—though at least simple life may be possible for brown dwarfs, white dwarfs, and neutron stars.
Star-like objects below 0.08 solar masses will end their lives as cold brown dwarfs.
Stars between 0.08 and 8 solar masses will evolve through various stages (blue dwarfs, red giants, and AGB stars) and then end their lives as white dwarfs.
Stars above 8 solar masses will end their lives in a supernova or direct collapse, resulting in a neutron star, black hole, or no remnant.
Stars often form multiple-star systems, though more massive stars do so more frequently.
All known multiple star systems are hierarchal arrangements of binary orbits.
A planet can appear in a multiple star system orbiting one star (S-type), orbiting the system barycenter (P-type) or co-orbital with one of the stars (T-type), all of which could be habitable.

Notes

Some of you may already be complaining that my definitions for habitability and complex life are too restrictive. I promise that I’ll look into alternatives to this paradigm of habitability in a later post, but for now I’m assuming that we want to create a world with liquid water on the surface and a biosphere based on photosynthesis.

It can get a bit confusing talking about "larger" and "smaller" stars when mass and size (in terms of radius/volume) are not always correlated. I've tried to avoid being ambiguous but to be clear, I mostly use "larger" and "smaller" to refer to mass, generally as comparisons between stars, but in a couple cases I refer to a single star becoming larger or smaller as it ages to refer to size (also, whenever I refer to a star as "light", I'm referring to its mass, not its luminosity or color).

See here⁵ for a more in-depth review of the habitability of M-type red dwarf stars.

The stated mass boundaries for different tracks of stellar evolution are all approximate; exact boundaries will vary depending on composition, and some aren’t hard boundaries (e.g. there’s likely to be some grey area between blue dwarfs and red giants). I’ve also seen different sources disagree on these boundaries, so I’ve gone with what seems to be the most consistent regime. Estimates for main sequence lifetime and spectral type based on mass seem to be pretty broad too; I can only assume that there’s a lot of variation between specific stars and some wiggle room in the definitions for these terms, as well as error in observations and models (Metallicity has an impact on both that I’ve largely glossed over).

The sun's effective temperature varies slightly over time, mostly based on the sunspot cycle between about 5770 and 5780 K, and so different sources will use slightly different values for the sun's temperature, but it's a negligible difference really.

~~Also, while we’re here, if anyone has an interest in neutron star formation and some skill in graphic design would you mind making a better diagram for the Wikipedia page?~~ Update: Someone actually did do this, thank you SimplisticReps.

Buy me a cup of tea (on Patreon)

Part III

1 Harre, J. V., & Heller, R. (2021). Digital color codes of stars. Astronomische Nachrichten, 342(3), 578-587.
2 Hills, J. G., & Dale, T. M. (1973). The nuclear fuel consumption of stars. The Astrophysical Journal, 185, 937-944.
3 Wood, A. J., Ackland, G. J., Dyke, J. G., Williams, H. T., & Lenton, T. M. (2008). Daisyworld: A review. Reviews of Geophysics, 46(1).
4 Rushby, A. J., Claire, M. W., Osborn, H., & Watson, A. J. (2013). Habitable zone lifetimes of exoplanets around main sequence stars. Astrobiology, 13(9), 833-849.
5 Shields, A. L., Ballard, S., & Johnson, J. A. (2016). The habitability of planets orbiting M-dwarf stars. Physics Reports, 663, 1-38.
6 Ramirez, R. M., & Kaltenegger, L. (2014). The habitable zones of pre-main-sequence stars. The Astrophysical Journal Letters, 797(2), L25.
7 Luger, R., & Barnes, R. (2015). Extreme water loss and abiotic O2 buildup on planets throughout the habitable zones of M dwarfs. Astrobiology, 15(2), 119-143.
8 Bolmont, E., Selsis, F., Owen, J. E., Ribas, I., Raymond, S. N., Leconte, J., & Gillon, M. (2017). Water loss from terrestrial planets orbiting ultracool dwarfs: implications for the planets of TRAPPIST-1. Monthly Notices of the Royal Astronomical Society, 464(3), 3728-3741.
9 "TRAPPIST-1 Planets Could Harbor 250 Times More Water Than Earth's Oceans", Space.com
10 Grimm, S. L., Demory, B. O., Gillon, M., Dorn, C., Agol, E., Burdanov, A., ... & Queloz, D. (2018). The nature of the TRAPPIST-1 exoplanets. Astronomy & Astrophysics, 613, A68.
11 Moore, K., & Cowan, N. B. (2020). Keeping M-Earths habitable in the face of atmospheric loss by sequestering water in the mantle. Monthly Notices of the Royal Astronomical Society, 496(3), 3786-3795.
12 Barnes, R., Mullins, K., Goldblatt, C., Meadows, V. S., Kasting, J. F., & Heller, R. (2013). Tidal Venuses: triggering a climate catastrophe via tidal heating. Astrobiology, 13(3), 225-250.
13 Luger, R., Barnes, R., Lopez, E., Fortney, J., Jackson, B., & Meadows, V. (2015). Habitable evaporated cores: transforming mini-Neptunes into super-Earths in the habitable zones of M dwarfs. Astrobiology, 15(1), 57-88.
14 O’Malley-James, J. T., & Kaltenegger, L. (2017). UV surface habitability of the TRAPPIST-1 system. Monthly Notices of the Royal Astronomical Society: Letters, 469(1), L26-L30.
15 Ilin, E., Poppenhaeger, K., Schmidt, S. J., Järvinen, S. P., Newton, E. R., Alvarado-Gómez, J. D., ... & Ilyin, I. (2021). Giant white-light flares on fully convective stars occur at high latitudes. Monthly Notices of the Royal Astronomical Society, 507(2), 1723-1745.
16 Pineda, J. S., Youngblood, A., & France, K. (2021). The Far Ultraviolet M-dwarf Evolution Survey. I. The Rotational Evolution of High-energy Emissions. The Astrophysical Journal, 911(2), 111.
17 Guo, J., Zhang, F., Zhang, X., & Han, Z. (2010). Habitable zones and UV habitable zones around host stars. Astrophysics and Space Science, 325(1), 25-30.
18 Kiang, N. Y., Segura, A., Tinetti, G., Blankenship, R. E., Cohen, M., Siefert, J., ... & Meadows, V. S. (2007). Spectral signatures of photosynthesis. II. Coevolution with other stars and the atmosphere on extrasolar worlds. Astrobiology, 7(1), 252-274.
19 Merlis, T. M., & Schneider, T. (2010). Atmospheric dynamics of Earth‐like tidally locked Aquaplanets. Journal of Advances in Modeling Earth Systems, 2(4).
20 Yang, J., Liu, Y., Hu, Y., & Abbot, D. S. (2014). Water trapping on tidally locked terrestrial planets requires special conditions. The Astrophysical Journal Letters, 796(2), L22.
21 Yang, J., Cowan, N. B., & Abbot, D. S. (2013). Stabilizing cloud feedback dramatically expands the habitable zone of tidally locked planets. The Astrophysical Journal Letters, 771(2), L45.
22 Leconte, J., Wu, H., Menou, K., & Murray, N. (2015). Asynchronous rotation of Earth-mass planets in the habitable zone of lower-mass stars. Science, 347(6222), 632-635.
23 Zanazzi, J. J., & Lai, D. (2017). Triaxial deformation and asynchronous rotation of rocky planets in the habitable zone of low-mass stars. Monthly Notices of the Royal Astronomical Society, 469(3), 2879-2885.
24 Wang, Y., Tian, F., & Hu, Y. (2014). Climate patterns of habitable exoplanets in eccentric orbits around m dwarfs. The Astrophysical Journal Letters, 791(1), L12.
25 Adams, F. C., Bodenheimer, P., & Laughlin, G. (2005). M dwarfs: planet formation and long term evolution. Astronomische Nachrichten: Astronomical Notes, 326(10), 913-919.
26 Yang, J., Ding, F., Ramirez, R. M., Peltier, W. R., Hu, Y., & Liu, Y. (2017). Abrupt climate transition of icy worlds from snowball to moist or runaway greenhouse. Nature Geoscience, 10(8), 556-560.
27 Agol, E. (2011). Transit surveys for Earths in the habitable zones of white dwarfs. The Astrophysical Journal Letters, 731(2), L31.
28 Nordhaus, J., & Spiegel, D. S. (2013). On the orbits of low-mass companions to white dwarfs and the fates of the known exoplanets. Monthly Notices of the Royal Astronomical Society, 432(1), 500-505.
29 Barnes, R., & Heller, R. (2013). Habitable planets around white and brown dwarfs: the perils of a cooling primary. Astrobiology, 13(3), 279-291.
30 von Bloh, W., Cuntz, M., Schröder, K. P., Bounama, C., & Franck, S. (2009). Habitability of super-Earth planets around other suns: models including red giant branch evolution. Astrobiology, 9(6), 593-602.
31 Ramirez, R. M., & Kaltenegger, L. (2016). Habitable zones of post-main sequence stars. The Astrophysical Journal, 823(1), 6.
32 Patruno, A., & Kama, M. (2017). Neutron star planets: Atmospheric processes and irradiation. Astronomy & Astrophysics, 608, A147.
33 Dai, D. C., Lue, A., Starkman, G., & Stojkovic, D. (2010). Electroweak stars: how nature may capitalize on the standard model's ultimate fuel. Journal of Cosmology and Astroparticle Physics, 2010(12), 004.
34 Ouyed, R., Dey, J., & Dey, M. (2002). Quark-nova. Astronomy & Astrophysics, 390(3), L39-L42.
35 Begelman, M. C., Rossi, E. M., & Armitage, P. J. (2008). Quasi-stars: accreting black holes inside massive envelopes. Monthly Notices of the Royal Astronomical Society, 387(4), 1649-1659.
36 Frankel, N. (2017). Nucleosynthesis in accretion disks around black holes. Lund Observatory Examensarbeten.
37 Wada, K., Tsukamoto, Y., & Kokubo, E. (2021). Formation of “Blanets” from Dust Grains around the Supermassive Black Holes in Galaxies. The Astrophysical Journal, 909(1), 96.
38 Lingam, M., Ginsburg, I., & Bialy, S. (2019). Active galactic nuclei: boon or bane for biota?. The Astrophysical Journal, 877(1), 62.
39 Iorio, L. (2020). What would happen if we were about 1 pc away from a supermassive black hole?. The Astrophysical Journal, 889(2), 152.
40 Opatrný, T., Richterek, L., & Bakala, P. (2017). Life under a black sun. American Journal of Physics, 85(1), 14-22.
41 Schnittman, J. D. (2019). Life on Miller's Planet: The Habitable Zone Around Supermassive Black Holes. arXiv preprint arXiv:1910.00940.
42 Bakala, P., Dočekal, J., & Turoňová, Z. (2020). Habitable zones around almost extremely spinning black holes (black sun revisited). The Astrophysical Journal, 889(1), 41.
43 Saumon, D., & Marley, M. S. (2008). The evolution of L and T dwarfs in color-magnitude diagrams. The Astrophysical Journal, 689(2), 1327.
44 Burrows, A., Hubbard, W. B., Lunine, J. I., & Liebert, J. (2001). The theory of brown dwarfs and extrasolar giant planets. Reviews of modern physics, 73(3), 719.
45 Adams, F. C., & Laughlin, G. (1997). A dying universe: the long-term fate and evolutionof astrophysical objects. Reviews of Modern Physics, 69(2), 337.
46 Homeier, D., Pinfield, D. J., Lodieu, N., Jones, H. R. A., Allard, F., & Pavlenko, Y. V. (2017). Primeval very low-mass stars and brown dwarfs–II. The most metal-poor substellar object. Monthly Notices of the Royal Astronomical Society, 468(1), 261-271.
47 "A theoretical and observational overview of brown dwarfs", Nicolas Lodieu
48 Duchêne, G., & Kraus, A. (2013). Stellar multiplicity. Annual Review of Astronomy and Astrophysics, 51, 269-310.
49 Quintana, E. V., & Lissauer, J. J. (2007). Terrestrial planet formation in binary star systems. arXiv preprint arXiv:0705.3444.
50 Kraus, A. L., Ireland, M. J., Huber, D., Mann, A. W., & Dupuy, T. J. (2016). The impact of stellar multiplicity on planetary systems. I. The ruinous influence of close binary companions. The Astronomical Journal, 152(1), 8.
51 Trilling, D. E., Stansberry, J. A., Stapelfeldt, K. R., Rieke, G. H., Su, K. Y. L., Gray, R. O., ... & Beichman, C. A. (2007). Debris disks in main-sequence binary systems. The Astrophysical Journal, 658(2), 1289.
52 Quarles, B., Li, G., & Lissauer, J. J. (2021). Milankovitch Cycles for a Circumstellar Earth-analog within 𝛼 Centauri-like Binaries. arXiv preprint arXiv:2108.12650.
53 Kaltenegger, L., & Haghighipour, N. (2013). Calculating the habitable zone of binary star systems. I. S-type binaries. The Astrophysical Journal, 777(2), 165.
54 Welsh, W. F., Orosz, J. A., Carter, J. A., & Fabrycky, D. C. (2012). Recent Kepler results on circumbinary planets. Proceedings of the International Astronomical Union, 8(S293), 125-132.
55 Fleming, D. P., Barnes, R., Graham, D. E., Luger, R., & Quinn, T. R. (2018). On the lack of circumbinary planets orbiting isolated binary stars. The Astrophysical Journal, 858(2), 86.
56 Childs, A. C., & Martin, R. G. (2021). Terrestrial planet formation in a circumbinary disc around a coplanar binary. Monthly Notices of the Royal Astronomical Society, 507(3), 3461-3472.
57 Doolin, S., & Blundell, K. M. (2011). The dynamics and stability of circumbinary orbits. Monthly Notices of the Royal Astronomical Society, 418(4), 2656-2668.
58 Popp, M., & Eggl, S. (2017). Climate variations on Earth-like circumbinary planets. Nature communications, 8(1), 1-12.
59 "Stability of Lagrange Points", Richard Fitzpatrick
60 Funk, B., Schwarz, R., Süli, A., & Érdi, B. (2012). On the stability of possible Trojan planets in the habitable zone: an application to the systems HD 147513 and HD 210277. Monthly Notices of the Royal Astronomical Society, 423(4), 3074-3082.
61 Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. (2009). Standing on the shoulders of giants-Trojan Earths and vortex trapping in low mass self-gravitating protoplanetary disks of gas and solids. Astronomy & Astrophysics, 493(3), 1125-1139.
62 Kiseleva, L. G., Eggleton, P. P., & Anosova, J. P. (1994). A note on the stability of hierarchical triple stars with initially circular orbits. Monthly Notices of the Royal Astronomical Society, 267(1), 161-166.
63 Eker, Z., Bakış, V., Bilir, S., Soydugan, F. A. R. U. K., Steer, I., Soydugan, E., ... & Alpsoy, M. (2018). Interrelated main-sequence mass–luminosity, mass–radius, and mass–effective temperature relations. Monthly Notices of the Royal Astronomical Society, 479(4), 5491-5511.
64 Yıldız, M. (2015). Grids of stellar models including second harmonic and colors: solar composition (Z= 0.0172, X= 0.7024). Research in Astronomy and Astrophysics, 15(12), 2244.
65 Rushby, A. J., Claire, M. W., Osborn, H., & Watson, A. J. (2013). Habitable zone lifetimes of exoplanets around main sequence stars. Astrobiology, 13(9), 833-849.
66 Guo, J., Zhang, F., Chen, X., & Han, Z. (2009). Probability distribution of terrestrial planets in habitable zones around host stars. Astrophysics and Space Science, 323(4), 367-373.
67 Hurley, J. R., Pols, O. R., & Tout, C. A. (2000). Comprehensive analytic formulae for stellar evolution as a function of mass and metallicity. Monthly Notices of the Royal Astronomical Society, 315(3), 543-569.
68 "A Modern Mean Dwarf Stellar Color and Effective Temperature Sequence" Eric Mamajek
69 Holman, M. J., & Wiegert, P. A. (1999). Long-term stability of planets in binary systems. The Astronomical Journal, 117(1), 621.

Previous Versions:

Before September 2021

Comments

AnonymousDecember 19, 2020 at 1:04 AM
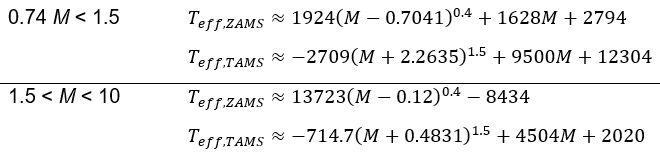
(sorry if i'm accidentally double-commenting) How could I calculate a planet's spin and orbit angular velocity to find its resonance? I skimmed the paper you linked on the topic and found the equation for that is spin angular velocity over orbit angular velocity? I bring this up because I have a planet with an eccentricity of 0.6, higher than any of the examples listed here.

Full feature list: mass = 2.9 Earth, semimajor axis is 0.23 AU, eccentricity is 0.6 as mentioned, and orbital parent has a mass of 0.65. I do not have a day length as of yet.
ReplyDelete
Replies
Rene KayJanuary 12, 2024 at 6:30 PM
Hi, I'm using your worldbuilding sheet to design a planet orbiting a close binary in a p-type orbit. Using the Hab Planet Temp I have to have the planet orbiting 0.65 AU from the binary stars, but the spreadsheets claims this is closer than the conservative habitable zone inner limit. I'm confused as to this discrepancy.
ReplyDelete
Replies
AnonymousMay 21, 2024 at 3:51 AM
Could a system with a star (of a mass similar to our Sun or less) that is in a wide binary orbit with a stellar-mass black hole, with a planet in an S-type orbit around the star, be habitable for simple life? If so, are there any other effects that the black hole would have on the planet and its life that I’d need to consider? Thank you in advance!
ReplyDelete
Replies

Add comment

Search This Blog

Worldbuilding Pasta

An Apple Pie From Scratch, Part II: Stars

Star Types

0.08-0.25 Solar Masses; Late M

Tidal-Locked Planets

Blue Dwarfs

White Dwarfs

0.25-0.8 Solar Masses; Early M to K

Red Giants

0.8-8 Solar Masses; G to Late B

Horizontal Branch and Asymptotic Giant Branch Stars

8-30 Solar Masses; Early B to Late O

Neutron Stars

>30 Solar Masses; Early O

Black Holes

0.013-0.08 Solar Masses; Y to Very Late M

Multiple-Star Systems

S-Type

P-Type

T-Type

Trinary

Calculating Stellar Properties

Simple Approximations

Complex Approximations

Evolutionary Models

Empirical Data

Binary System Orbits

Back Home

In Summary

Notes

Buy me a cup of tea (on Patreon)

Comments

Post a Comment

Popular Posts

Hurried Thoughts: You're Wrong About Tidal-Locking

An Apple Pie from Scratch, Part VIb: Climate: Biomes and Climate Zones